
【題目】如圖,等腰三角形ABC底邊BC的長(zhǎng)為4 cm,面積為12 cm2,腰AB的垂直平分線EF交AB于點(diǎn)E,交AC于點(diǎn)F,若D為BC邊上的中點(diǎn),M為線段EF上一點(diǎn),則△BDM的周長(zhǎng)最小值為( )
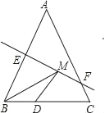
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
【答案】C
【解析】
連接AD,由于△ABC是等腰三角形,點(diǎn)D是BC邊的中點(diǎn),故AD⊥BC,再根據(jù)三角形的面積公式求出AD的長(zhǎng),再根據(jù)EF是線段AB的垂直平分線可知,點(diǎn)B關(guān)于直線EF的對(duì)稱(chēng)點(diǎn)為點(diǎn)A,故AD的長(zhǎng)為BM+MD的最小值,由此即可得出結(jié)論.
如圖,連接AD.
∵△ABC是等腰三角形,點(diǎn)D是BC邊的中點(diǎn),∴AD⊥BC,∴S△ABC=![]() BCAD=
BCAD=![]() ×4×AD=12,解得:AD=6(cm).
×4×AD=12,解得:AD=6(cm).
∵EF是線段AB的垂直平分線,∴點(diǎn)B關(guān)于直線EF的對(duì)稱(chēng)點(diǎn)為點(diǎn)A,∴AD的長(zhǎng)為BM+MD的最小值,∴△BDM的周長(zhǎng)最短=(BM+MD)+BD=AD+![]() BC=6+
BC=6+![]() ×4=6+2=8(cm).
×4=6+2=8(cm).
故選C.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】閱讀下列材料,并回答問(wèn)題.事實(shí)上,在任何一個(gè)直角三角形中,兩條直角邊的平方之和一定等于斜邊的平方,這個(gè)結(jié)論就是著名的勾股定理.請(qǐng)利用這個(gè)結(jié)論,完成下面活動(dòng):
![]() 一個(gè)直角三角形的兩條直角邊分別為
一個(gè)直角三角形的兩條直角邊分別為![]() ,那么這個(gè)直角三角形斜邊長(zhǎng)為____;
,那么這個(gè)直角三角形斜邊長(zhǎng)為____;
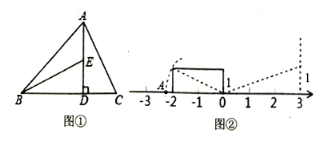
![]() 如圖①,
如圖①,![]() 于
于![]() ,求
,求![]() 的長(zhǎng)度;
的長(zhǎng)度;
![]() 如圖②,點(diǎn)
如圖②,點(diǎn)![]() 在數(shù)軸上表示的數(shù)是____請(qǐng)用類(lèi)似的方法在圖2數(shù)軸上畫(huà)出表示數(shù)
在數(shù)軸上表示的數(shù)是____請(qǐng)用類(lèi)似的方法在圖2數(shù)軸上畫(huà)出表示數(shù)![]() 的
的![]() 點(diǎn)(保留痕跡).
點(diǎn)(保留痕跡).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某物流公司引進(jìn)![]() ,
,![]() 兩種機(jī)器人用來(lái)搬運(yùn)某種貨物,這兩種機(jī)器人充滿電后可以連續(xù)搬運(yùn)
兩種機(jī)器人用來(lái)搬運(yùn)某種貨物,這兩種機(jī)器人充滿電后可以連續(xù)搬運(yùn)![]() 小時(shí),
小時(shí),![]() 種機(jī)器人于某日
種機(jī)器人于某日![]() 時(shí)開(kāi)始搬運(yùn),過(guò)了
時(shí)開(kāi)始搬運(yùn),過(guò)了![]() 小時(shí),
小時(shí),![]() 種機(jī)器人也開(kāi)始搬運(yùn),如圖,線段
種機(jī)器人也開(kāi)始搬運(yùn),如圖,線段![]() 表示
表示![]() 種機(jī)器人的搬運(yùn)量
種機(jī)器人的搬運(yùn)量![]() (千克)與時(shí)間
(千克)與時(shí)間![]() (時(shí))的函數(shù)圖像,線段
(時(shí))的函數(shù)圖像,線段![]() 表示
表示![]() 種機(jī)器人的搬運(yùn)量
種機(jī)器人的搬運(yùn)量![]() (千克)與時(shí)間
(千克)與時(shí)間![]() (時(shí))的函數(shù)圖像,根據(jù)圖像提供的信息,解答下列問(wèn)題:
(時(shí))的函數(shù)圖像,根據(jù)圖像提供的信息,解答下列問(wèn)題:

(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)如果![]() 、
、![]() 兩種機(jī)器人連續(xù)搬運(yùn)
兩種機(jī)器人連續(xù)搬運(yùn)![]() 個(gè)小時(shí),那么
個(gè)小時(shí),那么![]() 種機(jī)器人比
種機(jī)器人比![]() 種機(jī)器人多搬運(yùn)了多少千克?
種機(jī)器人多搬運(yùn)了多少千克?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,由6個(gè)長(zhǎng)為2,寬為1的小矩形組成的大矩形網(wǎng)格,小矩形的頂點(diǎn)稱(chēng)為這個(gè)矩形網(wǎng)格的格點(diǎn),由格點(diǎn)構(gòu)成的幾何圖形稱(chēng)為格點(diǎn)圖形(如:連接2個(gè)格點(diǎn),得到一條格點(diǎn)線段;連接3個(gè)格點(diǎn),得到一個(gè)格點(diǎn)三角形;…),請(qǐng)按要求作圖(標(biāo)出所畫(huà)圖形的頂點(diǎn)字母).
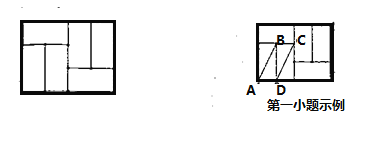
(1)畫(huà)出4種不同于示例的平行格點(diǎn)線段;

(2)畫(huà)出4種不同的成軸對(duì)稱(chēng)的格點(diǎn)三角形,并標(biāo)出其對(duì)稱(chēng)軸所在線段;

(3)畫(huà)出1個(gè)格點(diǎn)正方形,并簡(jiǎn)要證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在等邊![]() 中,
中,![]() 分別為
分別為![]() 的中點(diǎn),延長(zhǎng)
的中點(diǎn),延長(zhǎng)![]() 至點(diǎn)
至點(diǎn)![]() ,使
,使![]() ,連結(jié)
,連結(jié)![]() 和
和![]() .
.
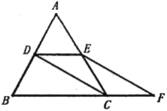
(1)求證:![]()
(2)猜想:![]() 的面積與四邊形
的面積與四邊形![]() 的面積的關(guān)系,并說(shuō)明理由.
的面積的關(guān)系,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司欲招聘廣告策劃人員一名,對(duì)甲、乙、丙三名候選人進(jìn)行三項(xiàng)素質(zhì)測(cè)試,他們的各項(xiàng)測(cè)試成績(jī)?nèi)缦卤硭荆?/span>
測(cè)試項(xiàng)目 | 測(cè)試成績(jī) | ||
甲 | 乙 | 丙 | |
創(chuàng)新 | 72 | 85 | 67 |
綜合知識(shí) | 50 | 74 | 70 |
語(yǔ)言 | 88 | 45 | 67 |
(1)如果根據(jù)三項(xiàng)測(cè)試的平均成績(jī)確定錄用人選,那么誰(shuí)將被錄用?
(2)根據(jù)實(shí)際需要,公司將創(chuàng)新、綜合知識(shí)、語(yǔ)言三項(xiàng)測(cè)試得分按5:3:2的比例確定各人的測(cè)試成績(jī),此時(shí)誰(shuí)將被錄用?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商場(chǎng)計(jì)劃購(gòu)進(jìn)A,B兩種新型節(jié)能臺(tái)燈共100盞,A型燈每盞進(jìn)價(jià)為30元,售價(jià)為45元;B型臺(tái)燈每盞進(jìn)價(jià)為50元,售價(jià)為70元.
(1)若商場(chǎng)預(yù)計(jì)進(jìn)貨款為3500元,求A型、B型節(jié)能燈各購(gòu)進(jìn)多少盞?
根據(jù)題意,先填寫(xiě)下表,再完成本問(wèn)解答:
型號(hào) | A型 | B型 |
購(gòu)進(jìn)數(shù)量(盞) | x | _____ |
購(gòu)買(mǎi)費(fèi)用(元) | _____ | _____ |
(2)若商場(chǎng)規(guī)定B型臺(tái)燈的進(jìn)貨數(shù)量不超過(guò)A型臺(tái)燈數(shù)量的3倍,應(yīng)怎樣進(jìn)貨才能使商場(chǎng)在銷(xiāo)售完這批臺(tái)燈時(shí)獲利最多?此時(shí)利潤(rùn)為多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)![]() 關(guān)于x軸的對(duì)稱(chēng)點(diǎn)和點(diǎn)
關(guān)于x軸的對(duì)稱(chēng)點(diǎn)和點(diǎn)![]() 關(guān)于y軸的對(duì)稱(chēng)點(diǎn)相同,則點(diǎn)
關(guān)于y軸的對(duì)稱(chēng)點(diǎn)相同,則點(diǎn)![]() 關(guān)于x軸對(duì)稱(chēng)的點(diǎn)的坐標(biāo)為( )
關(guān)于x軸對(duì)稱(chēng)的點(diǎn)的坐標(biāo)為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
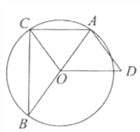
【題目】如圖,已知△ABC內(nèi)接于![]() ,AB是直徑,OD∥AC,AD=OC.
,AB是直徑,OD∥AC,AD=OC.
(1)求證:四邊形OCAD是平行四邊形;
(2)填空:①當(dāng)∠B= 時(shí),四邊形OCAD是菱形;
②當(dāng)∠B= 時(shí),AD與![]() 相切.
相切.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com