
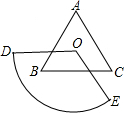
 ABC與扇形重疊部分的面積總等于△ABC的面積的
ABC與扇形重疊部分的面積總等于△ABC的面積的 ,扇形的圓心角應為多少度?說明你的理由.
,扇形的圓心角應為多少度?說明你的理由.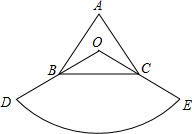 解:當扇形的圓心角為120°時,△ABC與扇形重疊部分的面積,總等于△ABC的面積的
解:當扇形的圓心角為120°時,△ABC與扇形重疊部分的面積,總等于△ABC的面積的 .
. ;
; ×360°=120°(等邊三角形的中心角等于
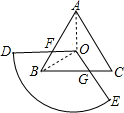
×360°=120°(等邊三角形的中心角等于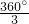 ),
),
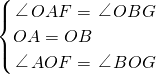 ,
, S△ABC,
S△ABC, ,
, .
. ,可以先從三角形考慮,O為中心也就是與正三角形的中心角重合,所以應為120°,證明是要分兩種情況:即特殊和一般,特殊情況時就是猜想所用的情況,顯然成立,一般情況的證明從三角形全等把四邊形的面積分解成兩個三角形,最后再歸到正三角形的中心角為120°的三角形.
,可以先從三角形考慮,O為中心也就是與正三角形的中心角重合,所以應為120°,證明是要分兩種情況:即特殊和一般,特殊情況時就是猜想所用的情況,顯然成立,一般情況的證明從三角形全等把四邊形的面積分解成兩個三角形,最后再歸到正三角形的中心角為120°的三角形.

 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案科目:初中數學 來源: 題型:
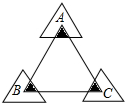 如圖,正三角形ABC的邊長為12,三個全等的小正三角形重心(即三條中線的交點)與正三角形ABC的頂點重合,且他們各有一邊與正三角形ABC的一邊平行.若小正三角形的邊長為x,且0<x≤12,陰影部分的面積為S,則能反映S與x之間函數關系的大致圖象是( )
如圖,正三角形ABC的邊長為12,三個全等的小正三角形重心(即三條中線的交點)與正三角形ABC的頂點重合,且他們各有一邊與正三角形ABC的一邊平行.若小正三角形的邊長為x,且0<x≤12,陰影部分的面積為S,則能反映S與x之間函數關系的大致圖象是( )A、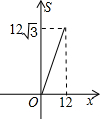 | B、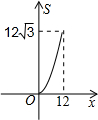 | C、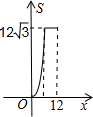 | D、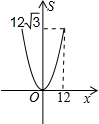 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| n | 1 | 2 | 3 | 4 |
| ln |
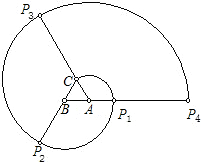
查看答案和解析>>
科目:初中數學 來源: 題型:
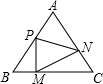 如圖,正三角形ABC的邊長為l,點M,N,P分別在邊BC,AB上,設BM=x,CN=y,AP=z,且x+y+z=1.
如圖,正三角形ABC的邊長為l,點M,N,P分別在邊BC,AB上,設BM=x,CN=y,AP=z,且x+y+z=1.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•十堰)如圖,正三角形ABC的邊長是2,分別以點B,C為圓心,以r為半徑作兩條弧,設兩弧與邊BC圍成的陰影部分面積為S,當
(2013•十堰)如圖,正三角形ABC的邊長是2,分別以點B,C為圓心,以r為半徑作兩條弧,設兩弧與邊BC圍成的陰影部分面積為S,當| 2 |
| π |
| 2 |
| 4π |
| 3 |
| 3 |
| π |
| 2 |
| 4π |
| 3 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com