【題目】如圖，半圓O與等腰直角三角形兩腰CA，CB分別切于D，E兩點，直徑FG在AB上，若BG＝
－1，則△ABC的周長為( )
A. 4＋2 B. 6 C. 2＋2 D. 4
【答案】A
【解析】
連接OD，OE，證四邊形ODCE是正方形，△OEB是等腰直角三角形，設OE=r，則BE=OG=r，建立關于r的方程，即可求解
解：如圖，連接OD，OE，
∵半圓O與等腰直角三角形兩腰CA、CB分別切于D、E兩點，
∴∠C=∠OEB=∠OEC=∠ODC=90°，∴四邊形ODCE是矩形。
∵OD=OE，∴四邊形ODCE是正方形。∴CD=CE=OE。
∵∠A=∠B=45°，∴△OEB是等腰直角三角形。
設OE=r，則BE=OG=r。∴OB=OG+BG=
﹣1+r。
∵OB=OE=r，∴﹣1+r=r，解得r=1。
∴AC=BC=2r=2，AB=2OB=2×（1+﹣1）=2。
∴△ABC的周長為：AC+BC+AB=4+2。
故選A.
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目：初中數學 來源： 題型：
【題目】如圖，AB＝16，O為AB中點，點C在線段OB上（不與點O，B重合），將OC繞點O逆時針旋轉270°后得到扇形COD，AP，BQ分別切優弧
于點P，Q，且點P， Q在AB異側，連接OP．
（1）求證：AP＝BQ；
（2）當BQ＝4
時，求扇形COQ的面積及
的長（結果保留π）；
（3）若△APO的外心在扇形COD的內部，請直接寫出OC的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知反比例函數y=
的圖象的一支位于第一象限，點A（x1，y1），B（x2，y2）都在該函數的圖象上．
（1）m的取值范圍是 ，函數圖象的另一支位于第一象限，若x1＞x2，y1＞y2，則點B在第 象限；
（2）如圖，O為坐標原點，點A在該反比例函數位于第一象限的圖象上，點C與點A關于x軸對稱，若△OAC的面積為6，求m的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】畫出函數y＝2x+1的圖象，利用圖象求：
（1）方程2x+1＝0的根；
（2）不等式2x+1≥0的解集；
（3）當y≤3時，求x的取值范圍；
（4）當﹣3≤y≤3時，求x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】矩形OABC的頂點A(-8，0)、C(0，6)，點D是BC邊上的中點，拋物線y=ax2+bx經過A、D兩點，如圖所示.
(1)求點D關于y軸的對稱點D′的坐標及a、b的值；
(2)在y軸上取一點P,使PA+PD長度最短,求點P的坐標；
(3)將拋物線y=ax2+bx向下平移,記平移后點A的對應點為A1，點D的對應點為D1，當拋物線平移到某個位置時，恰好使得點O是y軸上到A1、D1兩點距離之和OA1+OD1最短的一點，求此拋物線的解析式.
查看答案和解析>>
科目：初中數學 來源： 題型：
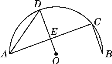
【題目】如圖，AB是半圓O的直徑，C，D是半圓O上的兩點，OD∥BC，OD與AC交于點E.
(1)若∠D＝70°，求∠CAD的度數；
(2)若AC＝8，DE＝2，求AB的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
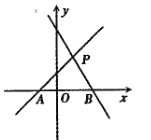
【題目】如圖，直線
是一次函數
的圖象，直線
是一次函數
的圖象.
（1）求A、B、P三點坐標；
（2）求
的面積；
（3）已知過P點的直線把分成面積相等的兩部分，求該直線解析式.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀理解：
為解方程（x2﹣1）2﹣5（x2﹣1）+4=0，我們可以將x2﹣1視為一個整體，然后設x2﹣1=y，則原方程化為y2﹣5y+4=0，解此方程得：y1=1，y2=4．
當y=1時，x2﹣1═1，∴x=±
．
當y=4時，x2﹣1═4，∴x=±
．
∴原方程的解為：x1=，x2=﹣，x3=，x4=﹣．
以上方法叫做換元法解方程，達到了降次的目的，體現了轉化思想．
運用上述方法解方程：x4﹣8x2+12=0．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
