
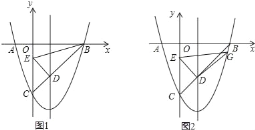
【題目】如圖,已知拋物線y=x2﹣2x﹣3經過x軸上的A,B兩點,與y軸交于點C,線段BC與拋物線的對稱軸相交于點D,點E為y軸上的一個動點.
(1)求直線BC的函數解析式,并求出點D的坐標;
(2)設點E的縱坐標為為m,在點E的運動過程中,當△BDE中為鈍角三角形時,求m的取值范圍;
(3)如圖2,連結DE,將射線DE繞點D順時針方向旋轉90°,與拋物線交點為G,連結EG,DG得到Rt△GED.在點E的運動過程中,是否存在這樣的Rt△GED,使得兩直角邊之比為2:1?如果存在,求出此時點G的坐標;如果不存在,請說明理由.
【答案】(1) y=x﹣3,D點坐標為(1,﹣2);(2) m>3或m<﹣1且m≠﹣3;(3)存在. G點坐標為(1![]() )或(3,0)或(1
)或(3,0)或(1![]() )或(﹣1,0).
)或(﹣1,0).
【解析】
(1)先根據拋物線與x軸的交點問題求出A(﹣1,0),B(3,0),利用對稱性可得拋物線的對稱軸為直線x=1,再求出C(0,﹣3),然后利用待定系數法求直線BC的解析式;當x=1時,y=x﹣3=﹣2,則D點坐標為(1,﹣2);
(2)如圖1,先判斷△OBC為等腰直角三角形,則∠OCB=∠OBC=45°,再計算出CD![]() ,然后通過求出△BDE為直角三角形時m的值來確定△BDE為鈍角三角形時m的取值范圍;
,然后通過求出△BDE為直角三角形時m的值來確定△BDE為鈍角三角形時m的取值范圍;
(3)分類討論:①當點G在對稱軸右側的拋物線上時,如圖2,作DF⊥y軸于F,GH⊥DF于H,設G(t,t2﹣2t﹣3),則GH=t2﹣2t﹣3﹣(﹣2)=t2﹣2t﹣1,由旋轉的性質得∠EDG=90°,接著證明Rt△EDF∽Rt△DGH,利用相似的性質得![]() ,分
,分![]() 2和
2和![]() ,列方程求出t的值,進而求出G的坐標;②當點G在對稱軸左側的拋物線上時,用同樣的方法可得G點坐標.
,列方程求出t的值,進而求出G的坐標;②當點G在對稱軸左側的拋物線上時,用同樣的方法可得G點坐標.
(1)當y=0時,x2﹣2x﹣3=0,解得:x1=﹣1,x2=3,則A(﹣1,0),B(3,0),所以拋物線的對稱軸為直線x=1,當x=0時,y=x2﹣2x﹣3=﹣3,則C(0,﹣3).
設直線BC的解析式為y=kx+b,把B(3,0),C(0,﹣3)代入得:![]() ,解得:
,解得:![]() ,所以直線BC的解析式為y=x﹣3;
,所以直線BC的解析式為y=x﹣3;
當x=1時,y=x﹣3=1﹣3=-2,則D點坐標為(1,﹣2);
(2)如圖1.
∵B(3,0),C(0,﹣3),∴△OBC為等腰直角三角形,∴∠OCB=∠OBC=45°.
∵D(1,﹣2),∴CD![]() ,當∠EDB=90°時,則△CDE為等腰直角三角形,∴CE
,當∠EDB=90°時,則△CDE為等腰直角三角形,∴CE![]() CD
CD![]() 2,∴OE=3﹣2=1,此時E(0,﹣1),∴當m<﹣1且m≠﹣3時,∠EDB為鈍角,△EDB為鈍角三角形;
2,∴OE=3﹣2=1,此時E(0,﹣1),∴當m<﹣1且m≠﹣3時,∠EDB為鈍角,△EDB為鈍角三角形;
當∠EBD=90°時,則△OBE為等腰直角三角形,∴OE=OB=3,此時E(0,3),∴當m>3時,∠EDB為鈍角,△EDB為鈍角三角形;
∴m的取值范圍為m>3或m<﹣1且m≠﹣3;
(3)存在.
①當點G在對稱軸右側的拋物線上時,如圖2,作DF⊥y軸于F,GH⊥DF于H,設G(t,t2﹣2t﹣3),則GH=t2﹣2t﹣3﹣(﹣2)=t2﹣2t﹣1.
∵射線DE繞點D順時針方向旋轉90°,與拋物線交點為G,∴∠EDG=90°,∴∠EDF+∠GDH=90°,而∠EDF+∠DEF=90°,∴∠DEF=∠GDH,∴Rt△EDF∽Rt△DGH,∴![]() ,分兩種情況討論:
,分兩種情況討論:
i)若![]() 2,則
2,則![]() 2,即t2﹣2t﹣1
2,即t2﹣2t﹣1![]() ,解得:t1=1
,解得:t1=1![]() (舍去),t2=1
(舍去),t2=1![]() ,此時G點坐標為(1
,此時G點坐標為(1![]() );
);
ii)若![]() ,則
,則![]() ,即t2﹣2t﹣1=2,解得:t1=﹣1(舍去),t2=3,此時G點坐標為(3,0);
,即t2﹣2t﹣1=2,解得:t1=﹣1(舍去),t2=3,此時G點坐標為(3,0);
②當點G在對稱軸左側的拋物線上時,用同樣的方法可得G點坐標為(1![]() )或(﹣1,0).
)或(﹣1,0).
綜上所述:G點坐標為(1![]() )或(3,0)或(1
)或(3,0)或(1![]() )或(﹣1,0).
)或(﹣1,0).


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:初中數學 來源: 題型:
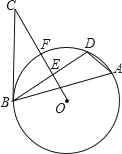
【題目】如圖,△ABD是⊙O的內接三角形,E是弦BD的中點,點C是⊙O外一點且∠DBC=∠A,連接OE延長與圓相交于點F,與BC相交于點C.
(1)求證:BC是⊙O的切線;
(2)若⊙O的半徑為6,BC=8,求弦BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
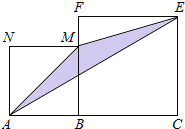
【題目】如圖,線段AC=n+1(其中n為正整數),點B在線段AC上,在線段AC同側作正方形ABMN及正方形BCEF,連接AM、ME、EA得到△AME.當AB=1時,△AME的面積記為S1;當AB=2時,△AME的面積記為S2;當AB=3時,△AME的面積記為
S3;則S3﹣S2= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】6月14日是“世界獻血日”,某市采取自愿報名的方式組織市民義務獻血.獻血時要對獻血者的血型進行檢測,檢測結果有“A型”、“B型”、“AB型”、“O型”4種類型.在獻血者人群中,隨機抽取了部分獻血者的血型結果進行統計,并根據這個統計結果制作了兩幅不完整的圖表:
血型 | A | B | AB | O |
人數 |
| 10 | 5 |
|
(1)這次隨機抽取的獻血者人數為 人,m= ;
(2)補全上表中的數據;
(3)若這次活動中該市有3000人義務獻血,請你根據抽樣結果回答:
從獻血者人群中任抽取一人,其血型是A型的概率是多少?并估計這3000人中大約有多少人是A型血?

查看答案和解析>>
科目:初中數學 來源: 題型:
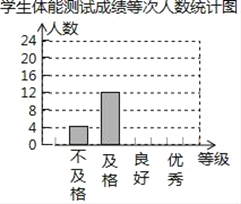
【題目】某校為了解學生體質情況,從各年級隨機抽取部分學生進行體能測試,每個學生的測試成績按標準對應為優秀、良好、及格、不及格四個等級,統計員在將測試數據繪制成圖表時發現,優秀漏統計4人,良好漏統計6人,于是及時更正,從而形成如圖圖表,請按正確數據解答下列各題:
學生體能測試成績各等次人數統計表
體能等級 | 調整前人數 | 調整后人數 |
優秀 | 8 |
|
良好 | 16 |
|
及格 | 12 |
|
不及格 | 4 |
|
合計 | 40 |
|
(1)填寫統計表;
(2)根據調整后數據,補全條形統計圖;
(3)若該校共有學生1500人,請你估算出該校體能測試等級為“優秀”的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我校第二課堂開展后受到了學生的追捧,學期結束后對部分學生做了一次“我最喜愛的第二課堂”問卷調查(每名學生都填了調査表,且只選了一個項目),統計后趣味數學、演講與口才、信息技術、手工制作榜上有名.其中選信息技術的人數比選手工制作的少8人;選趣味數學的人數不僅比選手工制作的人多,且為整數倍;選趣味數學與選手工制作的人數之和是選演講與口才與選信息技術的人數之和的5倍;選趣味數學與選演講與口才的人數之和比選信息技術與選手工制作的人數之和多24人.則參加調查問卷的學生有________人。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分5分)如圖,小明在大樓30米高
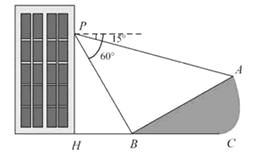
(即PH=30米)的窗口P處進行觀測,測得山
坡上A處的俯角為15°,山腳B處的俯角為
60°,已知該山坡的坡度i(即tan∠ABC)為1:
![]() ,點P、H、B、C、A在同一個平面上.點
,點P、H、B、C、A在同一個平面上.點
H、B、C在同一條直線上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度數等于 ▲ 度;
(2)求A、B兩點間的距離(結果精確到0.1米,參考數據:![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,D是BC的中點,過D點的直線GF交AC于F,交AC的平行線BG于G點,DE⊥DF,交AB于點E,連結EG、EF.

(1)求證:BG=CF.
(2)請你判斷BE+CF與EF的大小關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com