
【題目】如圖,△ABC中,AB=BC,BD⊥AC于點D,∠FAC=![]() ∠ABC,且∠FAC在AC下方.點P,Q分別是射線BD,射線AF上的動點,且點P不與點B重合,點Q不與點A重合,連接CQ,過點P作PE⊥CQ于點E,連接DE.
∠ABC,且∠FAC在AC下方.點P,Q分別是射線BD,射線AF上的動點,且點P不與點B重合,點Q不與點A重合,連接CQ,過點P作PE⊥CQ于點E,連接DE.
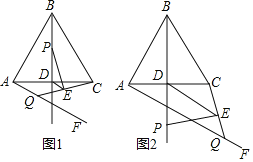
(1)若∠ABC=60°,BP=AQ.
①如圖1,當點P在線段BD上運動時,請直接寫出線段DE和線段AQ的數量關系和位置關系;
②如圖2,當點P運動到線段BD的延長線上時,試判斷①中的結論是否成立,并說明理由;
(2)若∠ABC=2α≠60°,請直接寫出當線段BP和線段AQ滿足什么數量關系時,能使(1)中①的結論仍然成立(用含α的三角函數表示).
【答案】(1)①DE=![]() AQ,DE∥AQ,理由見解析;② E∥AQ,DE=
AQ,DE∥AQ,理由見解析;② E∥AQ,DE=![]() AQ,理由見解析;(2)AQ=2BPsinα,理由見解析.
AQ,理由見解析;(2)AQ=2BPsinα,理由見解析.
【解析】
(1)①先判斷出△ABC是等邊三角形,進而判斷出∠CBP=∠CAQ,即可判斷出△BPC≌△AQC,再判斷出△PCQ是等邊三角形,進而得出CE=QE,即可得出結論;
②同①的方法即可得出結論;
(2)先判斷出,∠PAQ=90°﹣∠ACQ,∠BAP=90°﹣∠ACQ,進而得出∠BCP=∠ACQ,即可判斷出進而判斷出△BPC∽△AQC,最后用銳角三角函數即可得出結論.
(1)①DE=![]() AQ,DE∥AQ,
AQ,DE∥AQ,
理由:如圖1,連接PC,PQ,
在△ABC中,AB=AC,∠ABC=60°,
∴△ABC是等邊三角形,
∴∠ACB=60°,AC=BC,
∵AB=BC,BD⊥AC,
∴AD=CD,∠ABD=∠CBD=![]() ∠BAC,
∠BAC,
∵∠CAF=![]() ∠ABC,
∠ABC,
∴∠CBP=∠CAQ,
在△BPC和△AQC中,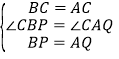 ,
,
∴△BPC≌△AQC(SAS),
∴PC=QC,∠BPC=∠ACQ,
∴∠PCQ=∠PCA+∠AQC=∠PCA+∠BCP=∠ACB=60°,
∴△PCQ是等邊三角形,
∵PE⊥CQ,
∴CE=QE,
∵AD=CD,
∴DE=![]() AQ,DE∥AQ;
AQ,DE∥AQ;
②DE∥AQ,DE=![]() AQ,
AQ,
理由:如圖2,連接PQ,PC,
同①的方法得出DE∥AQ,DE=![]() AQ;
AQ;
(2)AQ=2BPsinα,
理由:連接PQ,PC,
要使DE=![]() AQ,DE∥AQ,
AQ,DE∥AQ,
∵AD=CD,
∴CE=QE,
∵PE⊥CQ,
∴PQ=PC,
易知,PA=PC,
∴PA=PE=PC
∴以點P為圓心,PA為半徑的圓必過A,Q,C,
∴∠APQ=2∠ACQ,
∵PA=PQ,
∴∠PAQ=∠PQA=![]() (180°﹣∠APQ)=90°﹣∠ACQ,
(180°﹣∠APQ)=90°﹣∠ACQ,
∵∠CAF=∠ABD,∠ABD+∠BAD=90°,
∴∠BAQ=90°,
∴∠BAP=90°﹣∠PAQ=90°﹣∠ACQ,
易知,∠BCP=∠BAP,
∴∠BCP=∠ACQ,
∵∠CBP=∠CAQ,
∴△BPC∽△AQC,
∴![]() ,
,
在Rt△BCD中,sinα=![]() ,
,
∴![]() =2×
=2×![]() =2sinα,
=2sinα,
∴AQ=2BPsinα.


科目:初中數學 來源: 題型:
【題目】速度分別為100km/h和akm/h(0<a<100)的兩車分別從相距s千米的兩地同時出發,沿同一方向勻速前行.行駛一段時間后,其中一車按原速度原路返回,直到與另一車相遇時兩車停止.在此過程中,兩車之間的距離y(km)與行駛時間t(h)之間的函數關系如圖所示.下列說法:①a=60;②b=2;③c=b+![]() ;④若s=60,則b=
;④若s=60,則b=![]() .其中說法正確的是( )
.其中說法正確的是( )

A.①②③B.②③④C.①②④D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
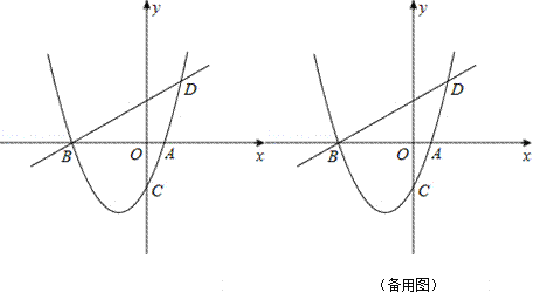
【題目】如圖,已知拋物線y=ax2+bx﹣2(a≠0)與x軸交于A、B兩點,與y軸交于C點,直線BD交拋物線于點D,并且D(2,3),tan∠DBA=![]() .
.
(1)求拋物線的解析式;
(2)已知點M為拋物線上一動點,且在第三象限,順次連接點B、M、C、A,求四邊形BMCA面積的最大值;
(3)在(2)中四邊形BMCA面積最大的條件下,過點M作直線平行于y軸,在這條直線上是否存在一個以Q點為圓心,OQ為半徑且與直線AC相切的圓?若存在,求出圓心Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
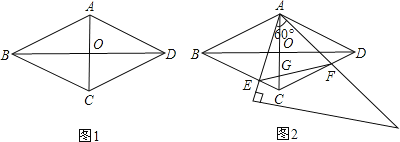
【題目】如圖1,在菱形ABCD中,AC=2,BD=2 3 ,AC,BD相交于點O.
(1)求邊AB的長;
(2)如圖2,將一個足夠大的直角三角板60°角的頂點放在菱形ABCD的頂點A處,繞點A左右旋轉,其中三角板60°角的兩邊分別與邊BC,CD相交于點E,F,連接EF與AC相交于點G.
①判斷△AEF是哪一種特殊三角形,并說明理由;
②旋轉過程中,當點E為邊BC的四等分點時(BE>CE),求CG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一家商店要進行裝修,若請甲、乙兩個裝修組同時施工,8天可以完成,需付兩組費用共3520元;若先請甲組單獨做6天,再請乙組單獨做12天可完成,需付兩組費用共3480元,問:
(1)甲、乙兩組工作一天,商店應各付多少元?
(2)已知甲組單獨做需12天完成,乙組單獨做需24天完成,單獨請哪組,商店所付費用最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+bx+c和直線y=x+1交于A,B兩點,點A在x軸上,點B在直線x=3上,直線x=3與x軸交于點C

(1)求拋物線的解析式;
(2)點P從點A出發,以每秒![]() 個單位長度的速度沿線段AB向點B運動,點Q從點C出發,以每秒2個單位長度的速度沿線段CA向點A運動,點P,Q同時出發,當其中一點到達終點時,另一個點也隨之停止運動,設運動時間為t秒(t>0).以PQ為邊作矩形PQNM,使點N在直線x=3上.
個單位長度的速度沿線段AB向點B運動,點Q從點C出發,以每秒2個單位長度的速度沿線段CA向點A運動,點P,Q同時出發,當其中一點到達終點時,另一個點也隨之停止運動,設運動時間為t秒(t>0).以PQ為邊作矩形PQNM,使點N在直線x=3上.
①當t為何值時,矩形PQNM的面積最小?并求出最小面積;
②直接寫出當t為何值時,恰好有矩形PQNM的頂點落在拋物線上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠BAD=60°,AC與BD交于點O,E為CD延長線上的一點,且CD=DE,連接BE分別交AC、AD于點F、G,連接OG,則下列結論中一定成立的是( )
①OG=![]() AB;②與△EGD全等的三角形共有5個;③S四邊形ODGF>S△ABF;④由點A、B、D、E構成的四邊形是菱形.
AB;②與△EGD全等的三角形共有5個;③S四邊形ODGF>S△ABF;④由點A、B、D、E構成的四邊形是菱形.
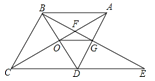
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABE、△ADC和△ABC分別是關于AB,AC邊所在直線的軸對稱圖形,若∠1:∠2:∠3=7:2:1,則∠α的度數為( ).

A.126°B.110°C.108°D.90°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC 中,AB=AC,∠BAC 的角平分線與∠ABC 的角平分線交于點 D,若∠ADB=130°,∠C=( )
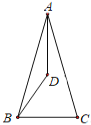
A.50°B.65°C.80°D.100°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com