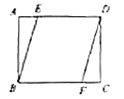
【題目】如圖，矩形
中，
，
，
、
分別是邊
、
上的點，
且
與
之間的距離為4，則
的長為（ ）
A. 3B. 
C. 
D. 
【答案】D
【解析】
過點D作DG⊥BE，垂足為G，則GD＝4＝AB，∠G＝90°，再利用AAS證明△AEB≌△GED，根據全等三角形的性質可得AE＝EG． 設AE＝EG＝x，則ED＝5﹣x，在Rt△DEG中，由勾股定理得可得方程x2+42＝（5﹣x）2， 解方程求得x的值即可得AE的長．
過點D作DG⊥BE，垂足為G，如圖所示：
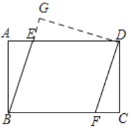
則GD＝4＝AB，∠G＝90°，
∵四邊形ABCD是矩形，
∴AD＝BC＝5，∠A＝90°＝∠G，
在△AEB和△GED中，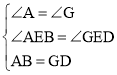
∴△AEB≌△GED（AAS）．
∴AE＝EG．
設AE＝EG＝x，則ED＝5﹣x，
在Rt△DEG中，由勾股定理得：ED2＝EG2+GD2，
∴x2+42＝（5﹣x）2，
解得：x＝
，即AE＝．
故選D．
科目：初中數學 來源： 題型：
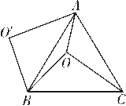
【題目】如圖，O是等邊△ABC內一點，OA=3，OB=4，OC=5，將線段BO以點B為旋轉中心逆時針旋轉60°得到線段BO′，下列結論：
①△BO′A可以由△BOC繞點B逆時針旋轉60°得到；&
②點O與O′的距離為4；
③∠AOB=150°；
④四邊形AOBO′的面積為6＋3
；
⑤S△AOC＋S△AOB=6＋
.
其中正確的結論是_______________．
查看答案和解析>>
科目：初中數學 來源： 題型：
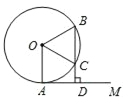
【題目】如圖，AM為⊙O的切線，A為切點，過⊙O上一點B作BD⊥AM于點D，BD交⊙O于C，OC平分∠AOB．
（1）求∠AOB的度數；
（2）若線段CD的長為2cm，求
的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知關于x的一元二次方程
，
（1）求證：該一元二次方程總有兩個實數根；
（2）若該方程只有一個小于4的根，求m的取值范圍；
（3）若x1，x2為方程的兩個根，且n＝x12+x22﹣4，判斷動點
所形成的數圖象是否經過點
，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
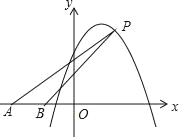
【題目】如圖，在平面直角坐標系中，點A、B的坐標分別為（﹣5，0）、（﹣2，0）．點P在拋物線y=﹣2x2+4x+8上，設點P的橫坐標為m．當0≤m≤3時，△PAB的面積S的取值范圍是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在直角坐標系xOy中，二次函數y=x2+（2k﹣1）x+k+1的圖象與x軸相交于O、A兩點．
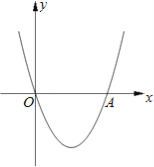
（1）求這個二次函數的解析式；
（2）在這條拋物線的對稱軸右邊的圖象上有一點B，使△AOB的面積等于6，求點B的坐標；
（3）對于（2）中的點B，在此拋物線上是否存在點P，使∠POB=90°？若存在，求出點P的坐標，并求出△POB的面積；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系中，一次函數
的圖象
分別與
，
軸交于
，
兩點，正比例函數的圖象
與交于點
．
（1）求
的值及的解析式；
（2）求
的值；
（3）一次函數
的圖象為
，且，，不能圍成三角形，直接寫出
的值．
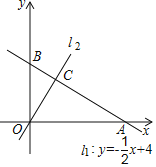
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在一個不透明的盒子里有5個小球，分別標有數字﹣3，﹣2，﹣1，﹣
，﹣
，這些小球除所標的數不同外其余都相同，先從盒子隨機摸出1個球，記下所標的數，再從剩下的球中隨機摸出1個球，記下所標的數．
（1）用畫樹狀圖或列表的方法求兩次摸出的球所標的數之積不大于1的概率．
（2）若以第一次摸出球上的數字為橫坐標，第二次摸出球上的數字為縱坐標確定一點，直接寫出該點在雙曲線y=
上的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在邊長為1個單位長度的小正方形組成的網格中，
的頂點均在格點上，點A的坐標為
，點B的坐標為
，點C的坐標為
.
（1）以點C為旋轉中心，將旋轉
后得到
，請畫出；
（2）平移，使點A的對應點
的坐標為
，請畫出
;
（3）若將繞點P旋轉可得到，則點P的坐標為___________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com