解:(1)∵拋物線y=ax
2+bx+c過點A(-1,0)點B(3,0),
∴設拋物線的解析式為y=a(x-1)(x-3),
∵OC=3OA,
∴C點的坐標為(0,-3),
把C的坐標代入y=a(x-1)(x-3),
解得a=1,
∴y=x
2-2x-3;
(2)由題意可知翻折后的拋物線的解析式為y=-x
2+2x+3,
①當直線過(3,0)時,b=3,當直線過(-1,0)時,b=-1,
∴當-1<b<3時,直線y=-x+b與翻折后的曲線的交點數為兩個;
②由
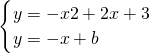
得:x2-3x+b-3=0,
∵直線y=-x+b與翻折后的曲線的交點數為兩個,
∴△=9-4(b-3)=0,
∴b=

,
綜上可知以及結合圖形可知當-1<b<3時或b>

時,直線和曲線有兩個交點;
(3)設直線AC的解析式為:y=kx+b,
則
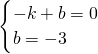
,
解得
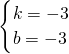
,
∴y=-3x-3,
當x=3時,y=-12,
∴D(3,-12)
∴(t+3)×4=15,
∴t=

,
即P的坐標為(0,

),
設平移后的拋物線解析式為y=(x-1)
2+m,
則當拋物線過點P時,

=(0-1)
2+m,
解得m=

,此時拋物線向上平移了

個單位,
當拋物線過D點時,-9=(-3+1)
2+m,
解得m=-13,
又因為-12=(3-1)
2+m,解得m=-16,此時拋物線向下平移了12個單位,
綜上可知拋物線最多向上平移

個單位,向下最多平移12個單位.
分析:(1)因為拋物線y=ax
2+bx+c過點A(-1,0)點B(3,0),所以可設拋物線的解析式為y=a(x-1)(x-3),由條件OC=3OA可知C的坐標為(0,-3),代入解析式y=a(x-1)(x-3)求出a的值即可;
(2)首先求出翻折后的拋物線的解析式,若直線y=-x+b與翻折后的曲線的交點數為兩個則當直線介于A,B之間可求出b的范圍或聯立兩個解析式組成的方程組有解也可以求出b的取值范圍;
(3)設直線AC的解析式為:y=kx+b,把A,C點的坐標分別代入求出直線的解析式,進而求出P點的坐標,若將拋物線沿其對稱軸上下平移,使拋物線與△PAD總有公共點,則可求出向上和向下時的m的最值即可.
點評:本題考查了用待定系數法求出二次函數和一次函數的解析式,一次函數和二次函數交點的個數以及二次函數的平移,題目的綜合性不小,難度中等.

 上,點C是拋物線與y軸的交點,且OC=3OA.
上,點C是拋物線與y軸的交點,且OC=3OA.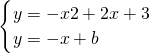 得:x2-3x+b-3=0,
得:x2-3x+b-3=0, ,
, 時,直線和曲線有兩個交點;
時,直線和曲線有兩個交點;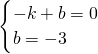 ,
,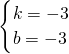 ,
, ,
, ),
), =(0-1)2+m,
=(0-1)2+m, ,此時拋物線向上平移了
,此時拋物線向上平移了 個單位,
個單位, 個單位,向下最多平移12個單位.
個單位,向下最多平移12個單位.

 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案

 (2012•陜西)如果一條拋物線y=ax2+bx+c(a≠0)與x軸有兩個交點,那么以該拋物線的頂點和這兩個交點為頂點的三角形稱為這條拋物線的“拋物線三角形”.
(2012•陜西)如果一條拋物線y=ax2+bx+c(a≠0)與x軸有兩個交點,那么以該拋物線的頂點和這兩個交點為頂點的三角形稱為這條拋物線的“拋物線三角形”.