
【題目】如圖,已知AM∥BN,∠A=60°,點P是射線AM上一動點(不與點A重合).BC、BD分別平分∠ABP和∠PBN,分別交射線AM于點C,D.
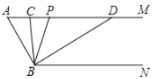
(發現)
(1)∵AM∥BN,∴∠ACB=_______;(填相等的角)
(2)求∠ABN、∠CBD的度數;
解:∵AM∥BN,
∴∠ABN+∠A=180°,
∵∠A=60°,
∴∠ABN=∠ABP+∠PBN=______,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=______,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=______.
(操作)
(3)當點P運動時,∠APB與∠ADB之間的數量關系是否隨之發生變化?若不變化,請寫出它們之間的關系,并說明理由;若變化,請寫出變化規律.
【答案】(1) ![]() ;(2)120°,
;(2)120°,![]() ,60°;(3)不變,
,60°;(3)不變,![]() ,理由見解析.
,理由見解析.
【解析】
(1)由平行線的性質:兩直線平行,內錯角相等即可得;
(2)根據平行線的性質及角平分線的定義即可;
(3)由平行線的性質及角平分線的定義即可.
解:(1)∵AM∥BN,
∴∠ACB=![]() ;
;
故答案為:![]()
(2)∵AM∥BN
∴∠ABN+∠A=180°,
∵∠A=60°,
∴∠ABN=120°,
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠PBD,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°.
故答案為:120°、![]() 、60°
、60°
(3)不變,![]() ,
,
理由:![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]()


科目:初中數學 來源: 題型:
【題目】如圖,四邊形OABC是矩形,四邊形ADEF是正方形,點A、D在x軸的負半軸上,點C在y軸的正半軸上,點F在AB上,點B、E在反比例函數![]() 的圖象上,正方形ADEF的面積為4,且BF=2AF,則k值為________.
的圖象上,正方形ADEF的面積為4,且BF=2AF,則k值為________.
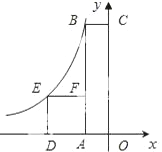
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB=6cm,AC=BD=4cm.∠CAB=∠DBA=60 ,點 P 在線段 AB 上以 1cm/s 的速度由點A 向點 B 運動,同時,點 Q 在線段 BD 上由點 B 向點 D 運動。它們運動的時間為 t(s),則點 Q的運動速度為________cm/s,使得 A. C. P 三點構成的三角形與 B. P、Q 三點構成的三角形全等。
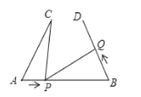
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C是線段AB的中點,延長線段AB至點D,使BD=AB,延長AD至點E,使DE=AC.
![]()
(1)依題意畫出圖形(尺規作圖),則![]() =_________(直接寫出結果);
=_________(直接寫出結果);
(2)若DE=3,求AB的長;
(3)請寫出與BE長度相同的線段.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD中,AB=2,∠C=60°,我們把菱形ABCD的對稱中心O稱作菱形的中心.菱形ABCD在直線l上向右作無滑動的翻滾,每繞著一個頂點旋轉60°叫一次操作,則經過1次這樣的操作菱形中心O所經過的路徑長為 ;經過3n(n為正整數)次這樣的操作菱形中心O所經過的路徑總長為 .(結果都保留π)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,蘭蘭站在河岸上的G點,看見河里有一只小船沿垂直于岸邊的方向劃過來,此時,測得小船C的俯角是∠FDC=30°,若蘭蘭的眼睛與地面的距離是1.5米,BG=1米,BG平行于AC所在的直線,迎水坡的坡度i=4:3,坡長AB=10米,求小船C到岸邊的距離CA的長?(參考數據:![]() =1.73,結果保留兩位有效數字)
=1.73,結果保留兩位有效數字)
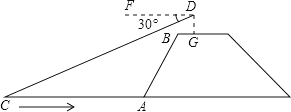
查看答案和解析>>
科目:初中數學 來源: 題型:
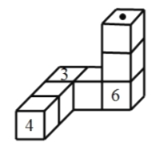
【題目】如圖,每個立方體的![]() 個面上分別寫有
個面上分別寫有![]() 到
到![]() 這
這![]() 個自然數,并且任意兩個相對面上所寫兩個數字之和為
個自然數,并且任意兩個相對面上所寫兩個數字之和為![]() ,把這樣的
,把這樣的![]() 個立方體一個挨著一個地連接起來,緊挨著兩個面上的數字之和為
個立方體一個挨著一個地連接起來,緊挨著兩個面上的數字之和為![]() ,則圖中“· ”所 在面上的數字是( )
,則圖中“· ”所 在面上的數字是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com