
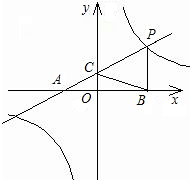
 如圖,點P是直線y=
如圖,點P是直線y=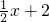 與雙曲線y=
與雙曲線y= 在第一象限內的一個交點,直線y=
在第一象限內的一個交點,直線y=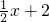 與x軸、y軸的交點分別為A、C,過P作PB垂直于x軸,若AB+PB=9.
與x軸、y軸的交點分別為A、C,過P作PB垂直于x軸,若AB+PB=9.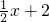 與x軸、y軸的交點,
與x軸、y軸的交點, x+2上的點,PB垂直于x軸,
x+2上的點,PB垂直于x軸, x+2),
x+2), x+2=
x+2= x+6,
x+6, x+6=9,解得,x=2,∴P點坐標為(2,3),
x+6=9,解得,x=2,∴P點坐標為(2,3), 上,
上, |AB||BP|-
|AB||BP|- |AB||OC|
|AB||OC| |AB|(|BP|-|OC|)=
|AB|(|BP|-|OC|)= |-4-2|(3-2)=
|-4-2|(3-2)= ×6=3.
×6=3. PB•OB=
PB•OB= ×2×3=3.
×2×3=3.

 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
 如圖,點A是直線y=-x+5和雙曲線y=
如圖,點A是直線y=-x+5和雙曲線y=| 6 |
| x |
A、4
| ||
| B、5 | ||
C、2
| ||
D、
|
查看答案和解析>>
科目:初中數學 來源: 題型:
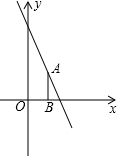 如圖,點A是直線y=-2x+3上的動點,過點A作AB垂直x軸于點B,y軸上存在點C,能使以A、B、C為頂點的三角形是等腰直角三角形.請寫出所有符合條件的點C的坐標
如圖,點A是直線y=-2x+3上的動點,過點A作AB垂直x軸于點B,y軸上存在點C,能使以A、B、C為頂點的三角形是等腰直角三角形.請寫出所有符合條件的點C的坐標查看答案和解析>>
科目:初中數學 來源: 題型:
 20、如圖,點O是直線AB上一點,OC平分∠AOB,在直線AB另一側以O為頂點作∠DOE=90°
20、如圖,點O是直線AB上一點,OC平分∠AOB,在直線AB另一側以O為頂點作∠DOE=90°查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,點P是直線m上一點,點Q是直線m外一點,
如圖,點P是直線m上一點,點Q是直線m外一點,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com