
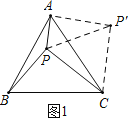
【題目】(1)閱讀理解:利用旋轉變換解決數學問題是一種常用的方法。如圖,點![]() 是等邊三角形
是等邊三角形![]() 內一點,
內一點,![]() ,求
,求![]() 的度數。為利用已知條件,不妨把
的度數。為利用已知條件,不妨把![]() 繞點
繞點![]() 順時針旋轉60°得
順時針旋轉60°得![]() ,連接
,連接![]() ,則
,則![]() 的長為_______;在
的長為_______;在![]() 中,易證
中,易證![]() ,且
,且![]() 的度數為_____,綜上可得
的度數為_____,綜上可得![]() 的度數為__ ;
的度數為__ ;
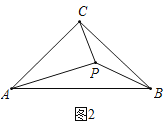
(2)類比遷移:如圖,點![]() 是等腰
是等腰![]() 內的一點,
內的一點,![]() 。求
。求![]() 的度數;
的度數;
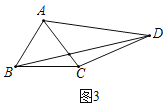
(3)拓展應用:如圖,在四邊形![]() 中,
中,![]() ,請直接寫出
,請直接寫出![]() 的長。
的長。
【答案】(1)2, 30°, 90° ;(2)90°;(3)2![]() .
.
【解析】
(1)由旋轉性質、等邊三角形的判定可知△CP′P是等邊三角形,由等邊三角形的性質知∠CP′P=60°,根據勾股定理逆定理可得△AP′P是直角三角形,繼而可得答案.
(2)如圖2,把△BPC繞點C順時針旋轉90°得△AP'C,連接PP′,同理可得△CP′P是等腰直角三角形和△AP′P是直角三角形,所以∠APC=90°;
(3)如圖3,將△ABD繞點A逆時針旋轉得到△ACG,連接DG.則BD=CG,根據勾股定理求CG的長,就可以得BD的長.
解:(1)把△BPC繞點C順時針旋轉60°得△AP'C,連接PP′(如圖1).
由旋轉的性質知△CP′P是等邊三角形;
∴P′A=PB=![]() 、∠CP′P=60°、P′P=PC=2,
、∠CP′P=60°、P′P=PC=2,
在△AP′P中,∵AP2+P′A2=12+(![]() )2=4=PP′2;
)2=4=PP′2;
∴△AP′P是直角三角形;
∴∠P′AP=90°.
∵PA=![]() PC,
PC,
∴∠AP′P=30°;
∴∠BPC=∠CP′A=∠CP′P+∠AP′P=60°+30°=90°.
故答案為:2;30°;90°;
(2)如圖2,把△BPC繞點C順時針旋轉90°得△AP'C,連接PP′.
由旋轉的性質知△CP′P是等腰直角三角形;
∴P′C=PC=1,∠CPP′=45°、P′P=![]() ,PB=AP'=
,PB=AP'=![]() ,
,
在△AP′P中,∵AP'2+P′P2=(![]() )2+(
)2+(![]() )2=2=AP2;
)2=2=AP2;
∴△AP′P是直角三角形;
∴∠AP′P=90°.
∴∠APP'=45°
∴∠APC=∠APP'+∠CPP'=45°+45°=90°
(3)如圖3,
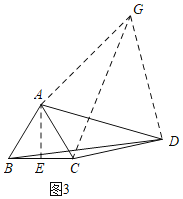
∵AB=AC,
將△ABD繞點A逆時針旋轉得到△ACG,連接DG.則BD=CG,
∵∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴△ABC∽△ADG,
∵AD=2AB,
∴DG=2BC=10,
過A作AE⊥BC于E,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADG+∠ADC=90°,
∴∠GDC=90°,
∴CG=![]() =
=![]() =2
=2![]() ,
,
∴BD=CG=2![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
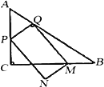
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 從點
從點![]() 出發,沿折線
出發,沿折線![]() 以每秒
以每秒![]() 個單位長度的速度向終點
個單位長度的速度向終點![]() 運動。當點
運動。當點![]() 不與點
不與點![]() 、
、![]() 重合時,在邊
重合時,在邊![]() 上取一點
上取一點![]() ,滿足
,滿足![]() ,過點
,過點![]() 作
作![]() ,交邊
,交邊![]() 于點
于點![]() ,以
,以![]() 、
、![]() 為邊做矩形
為邊做矩形![]() .設點
.設點![]() 的運動時間為
的運動時間為![]() 秒.
秒.
(1)用含![]() 的代數式表示線段
的代數式表示線段![]() 的長;
的長;
(2)當矩形![]() 為正方形時,求
為正方形時,求![]() 的值;
的值;
(3)設矩形![]() 與
與![]() 重疊部分圖形的周長為
重疊部分圖形的周長為![]() ,求
,求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(4)作點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() ,作點
,作點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() .當
.當![]() 、
、![]() 這兩點中只有一個點在矩形
這兩點中只有一個點在矩形![]() 內部時,直接寫出此時
內部時,直接寫出此時![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知等式![]() .
.
![]() 若等式中,已知
若等式中,已知![]() 是非零常量,請寫出因變量
是非零常量,請寫出因變量![]() 與自變量
與自變量![]() 的函數解析式;當
的函數解析式;當![]() 時,求
時,求![]() 的最大值和最小值及對應的
的最大值和最小值及對應的![]() 的取值.
的取值.
![]() 若等式中,
若等式中,![]() 是非零常量,請寫出因變量
是非零常量,請寫出因變量![]() 與自變量
與自變量![]() 的函數解析式,并判斷
的函數解析式,并判斷![]() 在什么范圍內取值時,
在什么范圍內取值時,![]() 隨
隨![]() 的增大而增大.
的增大而增大.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD放置在平面直角坐標系xOy中,已知A(-2,0),B(2,0),D(0,3),反比例函數y=![]() (x>0)的圖象經過點C.
(x>0)的圖象經過點C.
(1)求此反比例函數的解析式;
(2)問將平行四邊形ABCD向上平移多少個單位,能使點B落在雙曲線上?
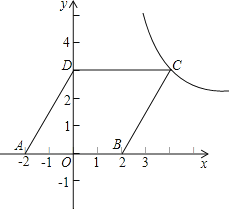
查看答案和解析>>
科目:初中數學 來源: 題型:
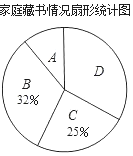
【題目】在“書香校園”活動中,某校為了解學生家庭藏書情況,隨機抽取本校部分學生進行調查,并繪制成部分統計圖表如下:
類別 | 家庭藏書m本 | 學生人數 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根據以上信息,解答下列問題:
(1)該調查的樣本容量為_____,a=_____;
(2)在扇形統計圖中,“A”對應扇形的圓心角為_____°;
(3)若該校有2000名學生,請估計全校學生中家庭藏書200本以上的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c的圖象與x軸的一個交點坐標是(3,0),對稱軸為直線x=1,下列結論:①abc>0;②2a+b=0;③4a﹣2b+c>0;④當y>0時,﹣1<x<3;⑤b<c.其中正確的個數是( )

A.2B.3C.4D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
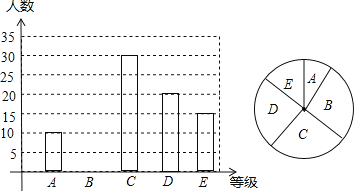
【題目】2019年,我省中考體育分值增加到55分,其中女生必考項目為八百米跑,我校現抽取九年級部分女生進行八百米測試成績如下:
成績 | 3′40″及以下 | 3′41~4′ | 4′01″~4′20′ | 4′21″~4′40″ | 4′41″及以上 |
等級 | A | B | C | D | E |
百分比 | 10% | 25% | m | 20% | n |
(1)求樣本容量及表格中的m和n的值
(2)求扇形統計圖中A等級所對的圓心角度數,并補全統計圖.
(3)我校9年級共有女生500人.若女生八百米成績的達標成績為4分,我校九年級女生八百米成績達標的人數有多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次數學綜合實踐活動中,小明計劃測量城門大樓的高度,在點B處測得樓頂A的仰角為22°,他正對著城樓前進21米到達C處,再登上3米高的樓臺D處,并測得此時樓頂A的仰角為45°.
(1)求城門大樓的高度;
(2)每逢重大節日,城門大樓管理處都要在A,B之間拉上繩子,并在繩子上掛一些彩旗,請你求出A,B之間所掛彩旗的長度(結果保留整數).(參考數據:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com