【題目】如圖，BP是△ABC中∠ABC的平分線，CP是∠ACB的外角的平分線，如果∠ABP=20°，∠ACP=50°，則∠A+∠P=（ ）
A.70°B.80°C.90°D.100°
期末沖刺100分創新金卷完全試卷系列答案科目：初中數學 來源： 題型：
【題目】為了解市民對“垃圾分類知識”的知曉程度,某數學學習興趣小組對市民進行隨機抽樣的問卷調查,調查結果分為“
.非常了解”、“
.了解”、“
.基本了解”、“
.不太了解”四個等級進行統計,并將統計結果繪制成如下兩幅不完整的統計圖(圖1,圖2),請根據圖中的信息解答下列問題.
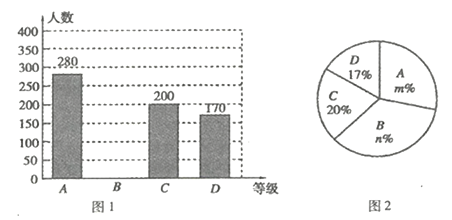
(1)這次調查的市民人數為 人,圖2中, 
；
(2)補全圖1中的條形統計圖；
(3)在圖2中的扇形統計圖中,求“.基本了解”所在扇形的圓心角度數；
(4)據統計,2018年該市約有市民500萬人,那么根據抽樣調查的結果,可估計對“垃圾分類知識”的知曉程度為“.不太了解”的市民約有多少萬人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，小螞蟻在9×9的小方格上沿著網格線運動（每小格邊長為1），一只螞蟻在C處找到食物后，要通知A、B、D、E處的其他小螞蟻，我們把它的行動規定：向上或向右為正，向下或向左為負。如果從C到D記為：C→D（＋2，－3）（第一個數表示左、右方向，第二個數表示上、下方向），那么；
（1）C→B（ ），C→E（ ），D→ （－4，－3），D→ （ ，＋3）；
（2）若這只小螞蟻的行走路線為C→E→D→B→A→C，請你計算小螞蟻走過的路程．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】 閱讀下面的材料
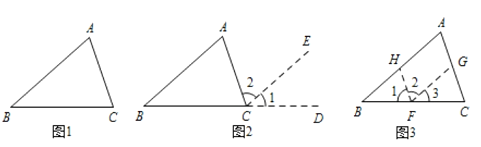
圖1，在△ABC中，試說明∠A+∠B+∠C=180°
通過畫平行線，將∠A、∠B、∠C作等量代換，使各角之和恰為一個平角，依輔助線不同而得多種方法：
解：如圖2，延長BC到點D，過點C作CE∥BA
因為BA∥CE（作圖所知）
所以∠B=∠2，∠A=∠1（兩直線平行，同位角、內錯角相等）
又因為∠BCD=∠BCA+∠2+∠1=180°（平角的定義）
所以∠A+∠B+∠ACB=180°（等量代換）
（1）如圖3，過BC上任一點F，作FH∥AC，FG∥AB，這種添加輔助線的方法能說∠A+∠B+∠C=180°嗎？并說明理由．
（2）還可以過點A作直線MN∥BC，或在三角形內取點P過P作三邊的平行線，請選擇一種方法，畫出相應圖形，并說明∠A+∠B+∠C=180°．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AD為△ABC的中線，BE為△ABD的中線．
(1)若∠ABE＝15°，∠BAD＝40°，則∠BED＝________°；
(2)請在圖中作出△BED中BD邊上的高EF；
(3)若△ABC的面積為40，BD＝5，則點E到BC邊的距離為多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點O是直線AB上一點，OD平分∠BOC，∠COE＝90°.
(1)若∠AOC＝36°，求∠DOE的度數；
(2)若∠AOC＝α，則∠DOE＝________.(用含α的代數式表示)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】根據李飛與劉亮射擊訓練的成績繪制了如圖所示的折線統計圖．
根據圖所提供的信息，若要推薦一位成績較穩定的選手去參賽，應推薦（ ）
A. 李飛或劉亮 B. 李飛 C. 劉亮 D. 無法確定
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為積極響應嘉興市垃圾分類工作的號召，大力倡導低碳生活，保護我們的生存環境．某校按抽樣規則抽取了部分學生進行垃圾分類的問卷調查(問卷內容如圖1)，答題情況如圖2所示．
（1）參與本次問卷調查的學生共有多少人?
（2）若該校共有800名學生，則估計該校全體學生中對垃圾分類非常清楚(即“全對”)的人數有多少?
（3）為講一步提高學生對垃圾分類的認識，學校加大了宣傳，一個月后按同樣的抽樣規則抽取與第一次樣本容量相等的學生進行第二次垃圾分類的問卷調查，答題情況如圖3所示．求前后兩次調查中答“全對”人數的增長率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
