解:(1)如圖,當y=0時,-

x+2=0,
解得x=3,
所以,點C的坐標為(3,4),
設乙蓄水池中水的深度y與注水時間x之間的函數關系式為y=kx+b,
則
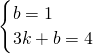
,
解得
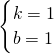
,
所以,函數關系式為y=x+1;
(2)聯立
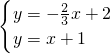
,
解得
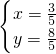
,
所以,交點A的坐標為(

,

),
表示的實際意義是:當注水時間為

小時,甲乙兩水池的水面高度相同,為

米,
故答案為:(

,

),當注水時間為

小時,甲乙兩水池的水面高度相同,為

米;
(3)設甲、乙兩個蓄水池的底面積分別為a、b,
根據甲乙兩水池的蓄水總量可得,2a+b=4b,
整理得,a=

b,
所以,當甲、乙兩個蓄水池的水的體積相等時,甲池中水的深度為
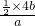
=
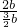
=

米.
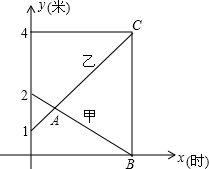
分析:(1)如圖,根據甲蓄水池的函數關系式求出放完水的時間,即函數圖象與x軸的交點B,從而得到乙圖象上的點C的坐標,然后利用待定系數法求一次函數解析式解答;
(2)聯立兩函數解析式,解方程組即可得到交點A的坐標,根據交點的縱坐標相等可知,兩水池的水面高度相等;
(3)設甲、乙兩蓄水池的底面積分別為a、b,根據開始時兩水池的水量等于結束時的乙水池的水量列式求出a、b的關系,然后用兩水池水量的一半除以甲水池的底面積,計算即可得解.
點評:本題考查了一次函數的應用,主要利用了一次函數圖象與坐標軸的交點的求法,待定系數法求一次函數解析式,以及函數圖象的交點的求解,(3)題要注意先求出兩蓄水池的底面積的關系是解題的關鍵.

 蓄水池中水的深度y(米)與注水時間x(時)之間的函數關系式為y=-
蓄水池中水的深度y(米)與注水時間x(時)之間的函數關系式為y=- x+2.結合圖象回答下列問題:
x+2.結合圖象回答下列問題: 解:(1)如圖,當y=0時,-
解:(1)如圖,當y=0時,- x+2=0,
x+2=0,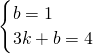 ,
,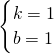 ,
,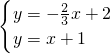 ,
,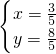 ,
, ,
, ),
), 小時,甲乙兩水池的水面高度相同,為
小時,甲乙兩水池的水面高度相同,為 米,
米, ,
, ),當注水時間為
),當注水時間為 小時,甲乙兩水池的水面高度相同,為
小時,甲乙兩水池的水面高度相同,為 米;
米; b,
b,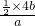 =
=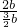 =
= 米.
米.

 53隨堂測系列答案
53隨堂測系列答案