
【題目】如圖,在平面直角坐標(biāo)系中,
(1)描出A(﹣4,3)、B(﹣1,0)、C(﹣2,3)三點(diǎn).
(2)△ABC 的面積是多少?
(3)作出△ABC 關(guān)于 y 軸的對(duì)稱圖形.
(4)請(qǐng)?jiān)?/span>x 軸上求作一點(diǎn)P,使△PA1C1 的周長(zhǎng)最小,并直接寫(xiě)出點(diǎn)P 的坐標(biāo)
【答案】(1)描點(diǎn)見(jiàn)解析;(2)3;(3)作圖見(jiàn)解析;(4)見(jiàn)解析,點(diǎn)P的坐標(biāo)為(3,0).
【解析】
利用A,B,C各點(diǎn)坐標(biāo)在平面坐標(biāo)系中描出即可;
利用三角形面積公式求出即可;
利用關(guān)于y軸對(duì)稱點(diǎn)的坐標(biāo)性質(zhì)進(jìn)而得出答案.
利用軸對(duì)稱求最短路線的方法得出P點(diǎn)位置.
(1)如圖所示:△ABC即為所求;
(2)△ABC的面積是:![]() ×2×3=3;
×2×3=3;
(3)如圖所示:△A1B1C1即為所求;
(4)如圖所示,作點(diǎn)A1關(guān)于y軸的對(duì)稱點(diǎn)Q,連接C1Q,交x軸于點(diǎn)P,則C1P=A1P,
∴△PA1C1的周長(zhǎng)最小值為A1C1+C1Q的長(zhǎng),此時(shí)點(diǎn)P的坐標(biāo)為(3,0).


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】解一元二次不等式 ![]() .
.
請(qǐng)按照下面的步驟,完成本題的解答.
解: ![]() 可化為
可化為 ![]() .
.
(1)依據(jù)“兩數(shù)相乘,同號(hào)得正”,可得不等式組①![]() 或不等式組②________.
或不等式組②________.
(2)解不等式組①,得________.
(3)解不等式組②,得________.
(4)一元二次不等式 ![]() 的解集為________.
的解集為________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是某地一座拋物線形拱橋,橋拱在豎直平面內(nèi),與水平橋面相交于A、B兩點(diǎn),拱橋最高點(diǎn)C到AB的距離為4m,AB=12m,D、E為拱橋底部的兩點(diǎn),且DE∥AB,點(diǎn)E到直線AB的距離為5m,則DE的長(zhǎng)為m. 
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】畫(huà)出函數(shù)![]() 的圖象,利用圖象求解下列問(wèn)題:
的圖象,利用圖象求解下列問(wèn)題:
(1)求方程![]() 的解;
的解;
(2)求不等式![]() 的解集;
的解集;
(3)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,二次函數(shù)y=ax2+bx+c的圖象與x軸交于(﹣2,0)和(4,0)兩點(diǎn),當(dāng)函數(shù)值y>0時(shí),自變量x的取值范圍是( ) 
A.x<﹣2
B.x>4
C.﹣2<x<4
D.x>0
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,△ABC中,∠CAB=90°,AC=AB,點(diǎn)D、E是BC上的兩點(diǎn),且∠DAE=45°,△ADC與△ADF關(guān)于直線AD對(duì)稱.
(1)求證:△AEF≌△AEB;
(2)∠DFE= °.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(10分)如圖,已知△ABC為等邊三角形,點(diǎn)D、E分別在BC、AC邊上,且AE=CD,AD與BE相交于點(diǎn)F。

(1)求證:△ABE≌△CAD;(2)求∠BFD的度數(shù)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
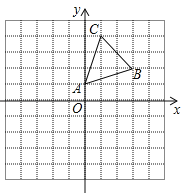
【題目】(2016甘肅省白銀市)如圖,在平面直角坐標(biāo)系中,△ABC的頂點(diǎn)A(0,1),B(3,2),C(1,4)均在正方形網(wǎng)格的格點(diǎn)上.
(1)畫(huà)出△ABC關(guān)于x軸的對(duì)稱圖形△A1B1C1;
(2)將△A1B1C1沿x軸方向向左平移3個(gè)單位后得到△A2B2C2,寫(xiě)出頂點(diǎn)A2,B2,C2的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】問(wèn)題背景
在△ABC中,AB,BC,AC的長(zhǎng)分別為![]() ,
,![]() ,
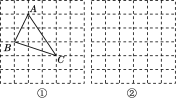
,![]() ,求這個(gè)三角形的面積.曉輝同學(xué)在解答這道題時(shí),先建立一個(gè)正方形網(wǎng)格(每個(gè)小正方形的邊長(zhǎng)為1),再在網(wǎng)格中畫(huà)出格點(diǎn)三角形ABC(即△ABC的三個(gè)頂點(diǎn)都在小正方形的頂點(diǎn)處),如圖①所示,這樣不需求△ABC的高,而借用網(wǎng)格就能計(jì)算出它的面積.
,求這個(gè)三角形的面積.曉輝同學(xué)在解答這道題時(shí),先建立一個(gè)正方形網(wǎng)格(每個(gè)小正方形的邊長(zhǎng)為1),再在網(wǎng)格中畫(huà)出格點(diǎn)三角形ABC(即△ABC的三個(gè)頂點(diǎn)都在小正方形的頂點(diǎn)處),如圖①所示,這樣不需求△ABC的高,而借用網(wǎng)格就能計(jì)算出它的面積.
(1)請(qǐng)你直接寫(xiě)出△ABC的面積:________.
(2)我們把上述求△ABC面積的方法叫做構(gòu)圖法.若△ABC的三邊長(zhǎng)分別為![]() a,2
a,2![]() a,
a,![]() a(a>0),請(qǐng)利用圖②的正方形網(wǎng)格(每個(gè)小正方形的邊長(zhǎng)為a)畫(huà)出相應(yīng)的△ABC,并求出它的面積.
a(a>0),請(qǐng)利用圖②的正方形網(wǎng)格(每個(gè)小正方形的邊長(zhǎng)為a)畫(huà)出相應(yīng)的△ABC,并求出它的面積.
探索創(chuàng)新
(3)若△ABC的三邊長(zhǎng)分別為![]() ,
,![]() ,2
,2![]() (m>0,n>0,且m≠n),試運(yùn)用構(gòu)圖法(自己重新設(shè)計(jì)一個(gè)符合結(jié)構(gòu)特征的網(wǎng)格)求出這個(gè)三角形的面積.
(m>0,n>0,且m≠n),試運(yùn)用構(gòu)圖法(自己重新設(shè)計(jì)一個(gè)符合結(jié)構(gòu)特征的網(wǎng)格)求出這個(gè)三角形的面積.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com