
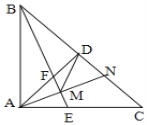
【題目】如圖,等腰![]() 中,
中,![]() =90°,
=90°,![]() 于
于![]() ,
,![]() 的平分線分別交
的平分線分別交![]() 、
、![]() 于
于![]() 、
、![]() 兩點,
兩點,![]() 為
為![]() 的中點,延長
的中點,延長![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .下列結論:①
.下列結論:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④![]() ;上述結論中正確的個數是( )
;上述結論中正確的個數是( )
A. 4個 B. 3個 C. 2個 D. 1個
【答案】A
【解析】
根據題意可得:AB=AC,∠BCA=∠ABC=45°=∠DAC=∠DAB,AD=BD=CD,AD⊥BC,即可證AE=AF,△ADN≌△BFD,△ABF≌△ANC,AM=MN;即可得結論.
解:∵等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,
∴AB=AC,∠BCA=∠ABC=45°=∠DAC=∠DAB,AD=BD=CD,AD⊥BC,
∵BE是平分∠ABC,
∴∠ABE=∠CBE=22.5°
∵AB⊥AC,AD⊥BC,
∴∠AEB=67.5°,∠AFD=67.5°=∠AFE,
∴∠AFE=∠AEB,
∴AF=AE,
故①正確,
∵M是EF的中點,AE=AF,
∴AM⊥BE,∠DAM=∠CAM=22.5°,
∴∠DAN=∠CBE=22.5°,且∠ADB=∠ADN,AD=BD,
∴△ADN≌△BDF
∴DF=DN,
故②正確,
∵AB=AC,∠ACB=∠DAB=45°,∠ABF=∠CAN=22.5°,
∴△ABF≌△CAN,
∴AF=CN,且AE=AF,
∴AE=CN,
故③正確,
∵∠BAN=∠BAD=∠DAN=67.5°,∠BNA=∠ACB+∠NAC=67.5°,
∴∠BAN=∠BNA,
∴BA=BN且AM⊥BE,
∴AM=MN,
∴△AMD和△DMN的面積相等,
故④正確,
故選:D.


科目:初中數學 來源: 題型:
【題目】我們把兩條中線互相垂直的三角形稱為“中垂三角形”,例如圖1,圖2,圖3中,AF,BE是△ABC的中線,AF⊥BE,垂足為P,像△ABC這樣的三角形均為“中垂三角形”,設BC=a,AC=b,AB=c.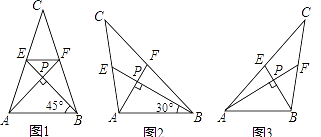
(1)【特例探索】
如圖1,當∠ABE=45°,c=2 ![]() 時,a= , b=;如圖2,當∠ABE=30°,c=4時,a= , b=;
時,a= , b=;如圖2,當∠ABE=30°,c=4時,a= , b=;
(2)【歸納證明】
請你觀察(1)中的計算結果,猜想a2 , b2 , c2三者之間的關系,用等式表示出來,請利用圖3證明你發現的關系式;
(3)【拓展應用】
如圖4,在ABCD中,點E,F,G分別是AD,BC,CD的中點,BE⊥EG,AD=2 ![]() ,AB=3.求AF的長.
,AB=3.求AF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線 ![]() 與x軸的負半軸交于點A,與y軸交于點B,連結AB.點C
與x軸的負半軸交于點A,與y軸交于點B,連結AB.點C ![]() 在拋物線上,直線AC與y軸交于點D.
在拋物線上,直線AC與y軸交于點D.
(1)求c的值及直線AC的函數表達式;
(2)點P在x軸的正半軸上,點Q在y軸正半軸上,連結PQ與直線AC交于點M,連結MO并延長交AB于點N,若M為PQ的中點.
①求證:△APM∽△AON;
②設點M的橫坐標為m , 求AN的長(用含m的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數 ![]() 的圖像與
的圖像與 ![]() 軸交于
軸交于 ![]() 、
、 ![]() 兩點,與
兩點,與 ![]() 軸交于點
軸交于點 ![]() ,
, ![]() .點
.點 ![]() 在函數圖像上,
在函數圖像上, ![]() 軸,且
軸,且 ![]() ,直線
,直線 ![]() 是拋物線的對稱軸,
是拋物線的對稱軸, ![]() 是拋物線的頂點.
是拋物線的頂點.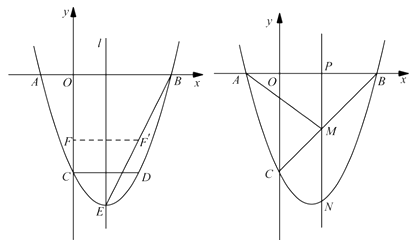
圖 ① 圖②
(1)求 ![]() 、
、 ![]() 的值;
的值;
(2)如圖①,連接 ![]() ,線段
,線段 ![]() 上的點
上的點 ![]() 關于直線
關于直線 ![]() 的對稱點
的對稱點 ![]() 恰好在線段
恰好在線段 ![]() 上,求點
上,求點 ![]() 的坐標;
的坐標;
(3)如圖②,動點 ![]() 在線段
在線段 ![]() 上,過點
上,過點 ![]() 作
作 ![]() 軸的垂線分別與
軸的垂線分別與 ![]() 交于點
交于點 ![]() ,與拋物線交于點
,與拋物線交于點 ![]() .試問:拋物線上是否存在點
.試問:拋物線上是否存在點 ![]() ,使得
,使得 ![]() 與
與 ![]() 的面積相等,且線段
的面積相等,且線段 ![]() 的長度最小?如果存在,求出點
的長度最小?如果存在,求出點 ![]() 的坐標;如果不存在,說明理由.
的坐標;如果不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在一次大課間活動中,采用了四鐘活動形式:A、跑步,B、跳繩,C、做操,D、游戲.全校學生都選擇了一種形式參與活動,小杰對同學們選用的活動形式進行了隨機抽樣調查,根據調查統計結果,繪制了不完整的統計圖. 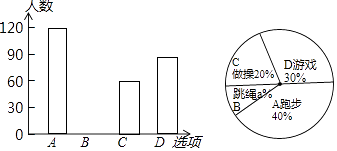
請結合統計圖,回答下列問題:
(1)本次調查學生共人,a= , 并將條形圖補充完整;
(2)如果該校有學生2000人,請你估計該校選擇“跑步”這種活動的學生約有多少人?
(3)學校讓每班在A、B、C、D四鐘活動形式中,隨機抽取兩種開展活動,請用樹狀圖或列表的方法,求每班抽取的兩種形式恰好是“跑步”和“跳繩”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將正整數 1 至 1050 按一定規律排列如下表:
1 | 2 | 3 | 4 | 5 | 6 | 7 |
8 | 9 | 10 | 11 | 12 | 13 | 14 |
15 | 16 | 17 | 18 | 19 | 20 | 21 |
22 | 23 | 24 | 25 | 26 | 27 | 28 |
29 | 30 | 31 | 32 | 33 | 34 | 35 |
從表中任取一個 3 3 的方框(如表中帶陰影的部分),方框中九個數的和可能是( )
A. 2025 B. 2018 C. 2016 D. 2007
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電信公司推出一款移動話費套餐,資費標準見下表:
套餐月費/元 | 套餐內容 | 套餐外資費 | |
主叫限定時間/分鐘 | 被叫 | 主叫超時費 (元/分鐘) | |
58 | 50 | 免費 | 0.25 |
88 | 150 | 0.20 | |
118 | 350 | 0.15 | |
說明:①主叫:主動打電話給別人;被叫:接聽別人打進來的電話. ②若辦理的是月使用費為 58 元的套餐,主叫時間不超過 50 分鐘時,當月話費即 為 58 元;主叫時間為 60 分鐘,則當月話費為 58+0.25×(60-50)=60.5 元. | |||
小文辦理的是月使用費為 88 元的套餐,亮亮辦理的是月使用費為 118 元的套餐.
(1)小文當月的主叫時間為 220 分鐘,則該月她的話費需多少元?
(2)某月小文和亮亮的主叫時間都為 m 分鐘 (m 350) ,請用含 m 的代數式表示該月他們的 話費差.
(3)某月小文和亮亮的話費相同,但主叫時間比亮亮少 100 分鐘,求小文和亮亮的主叫時間 分別為多少分鐘?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com