
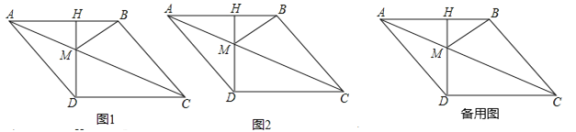
【題目】如圖1,四邊形ABCD是菱形,AD=10,過點D作AB的垂線DH,垂足為H,交對角線AC于M,連接BM,且AH=6.
(1)求證:DM=BM;
(2)求MH的長;
(3)如圖2,動點P從點A出發,沿折線ABC方向以2個單位/秒的速度向終點C勻速運動,設△PMB的面積為S(S≠0),點P的運動時間為t秒,求S與t之間的函數關系式;
(4)在(3)的條件下,當點P在邊AB上運動時是否存在這樣的t值,使∠MPB與∠BCD互為余角,若存在,則求出t值,若不存,在請說明理由.
【答案】(1)見解析;(2)3;(3)①當P在AB之間時,S=-3t+15;②當P在BC之間時,S=5t-25;(4)t=1.
【解析】
(1)由菱形的性質得,∠ACD=∠ACB,CD=CB,根據“SAS”證明△DCM≌△BCM,然后根據全等三角形的性質可得DM=BM;
(2)根據勾股定理即可得到結論;
(3)由△BCM≌△DCM計算出BM=DM,分兩種情況計算即可;
(4)由菱形的性質判斷出△ADM≌△ABM,再判斷出△BMP是等腰三角形,即可.
解:(1)在Rt△ADH中,AD=10,AH=6,
∴DH=8,
∵AC是菱形ABCD的對角線,
∴∠ACD=∠ACB,CD=CB,
在△DCM和△BCM中,
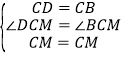 ,
,
∴△DCM≌△BCM(SAS),
∴DM=BM,
(2)在Rt△BHM中,BM=DM,HM=DH-DM=8-DM,BH=AB-AH=4,
根據勾股定理得,DM2-MH2=BH2,
即:DM2-(8-DM)2=16,
∴DM=5,
∴MH=3;
(3)在△BCM和△DCM中,
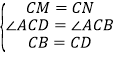 ,
,
∴△BCM≌△DCM(SAS),
∴BM=DM=5,∠CDM=∠CBM=90°
①當P在AB之間時,S=![]() (10-2t)×3=-3t+15;
(10-2t)×3=-3t+15;
②當P在BC之間時,S=![]() (2t-10)×5=5t-25;
(2t-10)×5=5t-25;
(4)存在,
∵∠ADM+∠BAD=90°,∠BCD=∠BAD,
∴∠ADM+∠BCD=90°,
∵∠MPB+∠BCD=90°,
∴∠MPB=∠ADM,
∵四邊形ABCD是菱形,
∴∠DAM=∠BAM,
∵AM=AM,
∴△ADM≌△ABM(SAS),
∴∠ADM=∠ABM,
∴∠MPB=∠ABM,
∵MH⊥AB,
∴PH=BH=4,
∴BP=2BH=8,
∵AB=10,
∴AP=2,
∴t=![]() =1
=1


科目:初中數學 來源: 題型:
【題目】已知:△ABC與△A'B'C在平面直角坐標系中的位置如圖.

(1)分別寫出B、B'的坐標:B______;B′______;
(2)若點P(a,b)是△ABC內部一點,則平移后△A'B'C內的對應點P′的坐標為______;
(3)求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解某市120000名初中學生的視力情況,某校數學興趣小組,并進行整理分析.
(1)小明在眼鏡店調查了1000名初中學生的視力,小剛在鄰居中調查了20名初中學生的視力,他們的抽樣是否合理?并說明理由.
(2)該校數學興趣小組從該市七、八、九年級各隨機抽取了1000名學生進行調查,整理他們的視力情況數據,得到如下的折線統計圖.
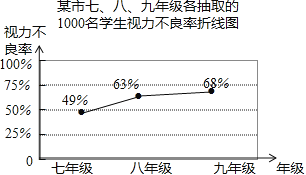
請你根據抽樣調查的結果,估計該市120000名初中學生視力不良的人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把6張長為a、寬為b(a>b)的小長方形紙片不重疊地放在長方形ABCD內,未被覆蓋的部分(兩個長方形)用陰影表示,設這兩個長方形的面積的差為S.當BC的長度變化時,按照同樣的放置方式,S始終保持不變,則a、b滿足( )

A. a=1.5bB. a=2.5bC. a=3bD. a=2b
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,
, ![]() 是一次函數
是一次函數![]() 的圖象和反比例函數
的圖象和反比例函數![]() 的圖象的兩個交點.
的圖象的兩個交點.
(1) 求一次函數、反比例函數的關系式;
(2) 求△AOB的面積.
(3) 當自變量x滿足什么條件時,y1>y2 .(直接寫出答案)
(4)將反比例函數![]() 的圖象向右平移n(n>0)個單位,得到的新圖象經過點(3,-4),求對應的函數關系式y3.(直接寫出答案)
的圖象向右平移n(n>0)個單位,得到的新圖象經過點(3,-4),求對應的函數關系式y3.(直接寫出答案)

查看答案和解析>>
科目:初中數學 來源: 題型:
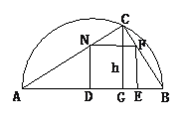
【題目】在直徑為AB的半圓內,劃出一塊三角形區域,如圖所示,使三角形的一邊為AB,頂點C在半圓圓周上,其它兩邊分別為6和8,現要建造一個內接于△ABC的矩形水池DEFN,其中D、E在AB上,如圖24-94的設計方案是使AC=8,BC=6.
(1)求△ABC的邊AB上的高h.
(2)設DN=x,且![]() ,當x取何值時,水池DEFN的面積最大?
,當x取何值時,水池DEFN的面積最大?
(3)實際施工時,發現在AB上距B點1.85的M處有一棵大樹,問:這棵大樹是否位于最大矩形水池的邊上?如果在,為了保護大樹,請設計出另外的方案,使內接于滿足條件的三角形中欲建的最大矩形水池能避開大樹.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙中每個小正方形的邊長都是1個單位長度,Rt△ABC的三個頂點A(-2,2),B(0,5),C(0,2).
(1)將△ABC以點C為旋轉中心旋轉180°,得到△A1B1C,請畫出△A1B1C的圖形.
(2)平移△ABC,使點A的對應點A2坐標為(-2,-6),請畫出平移后對應的△A2B2C2的圖形.
(3)若將△A1B1C繞某一點旋轉可得到△A2B2C2,請直接寫出旋轉中心的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,E是邊CD上一點(點E不與點C、D重合),連結BE.
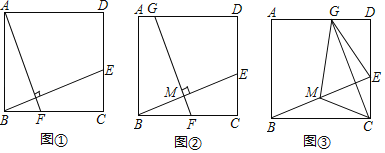
(感知)如圖①,過點A作AF⊥BE交BC于點F.易證△ABF≌△BCE.(不需要證明)
(探究)如圖②,取BE的中點M,過點M作FG⊥BE交BC于點F,交AD于點G.
(1)求證:BE=FG.
(2)連結CM,若CM=1,則FG的長為 .
(應用)如圖③,取BE的中點M,連結CM.過點C作CG⊥BE交AD于點G,連結EG、MG.若CM=3,則四邊形GMCE的面積為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
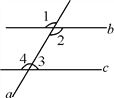
【題目】完成下面推理過程:
如圖,∠1+∠2=230°,b∥c,則∠1,∠2,∠3,∠4各是多少度?
解:∵∠1=∠2(__________________),
∠1+∠2=230°,
∴∠1=∠2=___________(填度數).
∵b∥c,
∴∠4=∠2=_______(填度數)(_______________________________),
∠2+∠3=180°(________________________________),
∴∠3=180°-∠2=____________(填度數).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com