
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() 于點E,
于點E,![]() 于點D,BE與AD相交于F.
于點D,BE與AD相交于F.
![]() 求證:
求證:![]() ;
;
![]() 若
若![]() ,求AF的長.
,求AF的長.

【答案】(1)證明見解析(2)AF=3![]()
【解析】
(1)根據(jù)等腰三角形腰長相等性質(zhì)可得AD=BD,即可求證△BDF≌△ACD,即可解答;
(2)連接CF,根據(jù)全等三角形的性質(zhì)得到DF=DC,得到△DFC是等腰直角三角形.推出AE=EC,BE是AC的垂直平分線.于是得到結(jié)論.
解:(1)AD⊥BD,∠BAD=45°,
∴AD=BD,
∵∠BFD=∠AFE,∠AFE+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠BFD=∠ACD,
在△BDF和△ACD中,
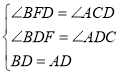
∴△BDF≌△ACD(AAS),
∴BF=AC;
(2)連接CF,
∵△BDF≌△ADC,
∴DF=DC,
∴△DFC是等腰直角三角形.
∵CD=3,CF=![]() CD=3
CD=3![]() ,
,
∵AB=BC,BE⊥AC,
∴AE=EC,BE是AC的垂直平分線.
∴AF=CF,
∴AF=3![]() .
.



科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,在一個長方形的草坪ABCD中,修了一條A-E-C的小路.AB=12米,BC=16米,AE=11米.極個別同學為了走“捷徑”,沿著AC路線行走,破壞草坪.
(1)請求出小路EC段的長度;
(2)請求出實際上這些同學僅僅少走了多少米?

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() ,與
,與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 經(jīng)過
經(jīng)過![]() ,
,![]() 兩點.
兩點.
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 在
在![]() 上方的拋物線上有一動點
上方的拋物線上有一動點![]() .
.
①如圖![]() ,當點
,當點![]() 運動到某位置時,以
運動到某位置時,以![]() ,
,![]() 為鄰邊的平行四邊形第四個頂點恰好也在拋物線上,求出此時點
為鄰邊的平行四邊形第四個頂點恰好也在拋物線上,求出此時點![]() 的坐標;
的坐標;
②如圖![]() ,過點
,過點![]() ,
,![]() 的直線
的直線![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知方程![]() .
.
![]() 若
若![]() ,求方程的根;
,求方程的根;
![]() 找出一組正整數(shù)
找出一組正整數(shù)![]() ,
,![]() ,使得方程的三個根均為整數(shù);
,使得方程的三個根均為整數(shù);
![]() 證明:只有一組正整數(shù)
證明:只有一組正整數(shù)![]() ,
,![]() ,使得方程的三個根均為整數(shù).
,使得方程的三個根均為整數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,![]() ≌
≌![]() ,
,![]() ≌
≌![]() ,B,E,C在一條直線上
,B,E,C在一條直線上![]() 下列結(jié)論:
下列結(jié)論:![]() 是
是![]() 的平分線;
的平分線;![]() ;
;![]() ;
;![]() 線段DE是
線段DE是![]() 的中線;
的中線;![]() 其中正確的有 ()個.
其中正確的有 ()個.

A.2B.3C.4D.5
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,二次函數(shù)![]() 的圖象與
的圖象與![]() 軸的一個交點是
軸的一個交點是![]() ,頂點是
,頂點是![]() ,根據(jù)
,根據(jù)

圖象回答下列問題:
![]() 當
當![]() ________時,
________時,![]() 隨
隨![]() 的增大而增大;
的增大而增大;
![]() 方程
方程![]() 的兩個根為________,方程
的兩個根為________,方程![]() 的根為________;
的根為________;
![]() 不等式
不等式![]() 的解集為________;
的解集為________;
![]() 若方程
若方程![]() 無解,則
無解,則![]() 的取值范圍為________.
的取值范圍為________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(本題10分)閱讀材料:分解因式:![]()
解:![]()
=![]()
=![]()
=![]()
=![]()
=![]() ,
,
此種方法抓住了二次項和一次項的特點,然后加一項,使三項成為完全平方式,我們把這種分解因式的方法叫配方法.
(1)用上述方法分解因式:![]() ;
;
(2)無論![]() 取何值,代數(shù)式
取何值,代數(shù)式![]() 總有一個最小值,請嘗試用配方法求出當
總有一個最小值,請嘗試用配方法求出當![]() 取何值時代數(shù)式的值最小,并求出這個最小值.
取何值時代數(shù)式的值最小,并求出這個最小值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com