
【題目】2018霧霾天氣趨于嚴重,某商場根據民眾健康需要,從廠家購進了A,B兩種型號的空氣凈化器,如果銷售15臺A型和10臺B型空氣凈化器的利潤為6000元,銷售10臺A型和15臺B型空氣凈化器的利潤為6500元.
(1)求每臺A型空氣凈化器和B型空氣凈化器的銷售利潤;
(2)該商場計劃一次購進兩種型號的空氣凈化器共160臺,其中B型空氣凈化器的進貨量不超過A型空氣凈化器的2倍,設購進A型空氣凈化器x臺,這160臺空氣凈化器的銷售總利潤為y元.
①求y關于x的函數關系式;
②該公司購進A型、B型空氣凈化器各多少臺時,才能使銷售總利潤最大?
【答案】(1) 每臺A型空氣凈化器得銷售利潤為200元,每臺B型空氣凈化器的銷售利潤為300元;(2)①y=100x+48000;②該公司購進A型、B型空氣凈化器分別為54臺、106臺時,才能使銷售總利潤最大.
【解析】
(1)根據題意可以列出相應的二元一次方程組,從而可以解答本題;
(2)①根據題意可以得到y與x的函數關系式;
②根據題意可以求得x的取值范圍,由①中的函數關系,從而可以得到該公司購進A型、B型空氣凈化器各多少臺時,才能使銷售總利潤最大.
(1)設每臺A型空氣凈化器得銷售利潤為a元,每臺B型空氣凈化器的銷售利潤為b元,
![]() ,得
,得![]() ,
,
即每臺A型空氣凈化器得銷售利潤為200元,每臺B型空氣凈化器的銷售利潤為300元;
(2)①由題意可得,y=200x+(160x)×300=100x+48000,
即y關于x的函數關系式是y=100x+48000;
②由題意可得,
160x2x,得![]() ,
,
∵y=100x+48000,
∴x=54時,y取得最大值,此時,160x=106,
即該公司購進A型、B型空氣凈化器分別為54臺、106臺時,才能使銷售總利潤最大.


科目:初中數學 來源: 題型:
【題目】2017年9月第18號臺風“泰利”給某地造成嚴重影響.草根救援隊駕若沖鋒舟沿一條東西方向的河流營救災民,早晨從![]() 地出發,晚上最后到達
地出發,晚上最后到達![]() 地,約定向東為正方向,當天航行依次記錄如下(單位:千米)
地,約定向東為正方向,當天航行依次記錄如下(單位:千米) ![]() 問:
問:
(1)![]() 地在
地在![]() 地的東面,還是西面?與
地的東面,還是西面?與![]() 地相距多少千米?
地相距多少千米?
(2)若沖鋒舟每千米耗油0.5升,每升汽油需6.8元,問沖鋒舟工作一天需汽油費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形 ABCD 中,∠BAD=α,∠BCD=180°-α,BD 平分∠ABC.
(1)如圖,若α=90°,根據教材中一個重要性質直接可得 DA=CD,這個性質是 ;

(2)問題解決:如圖,求證:AD=CD;

(3)問題拓展:如圖,在等腰△ABC 中,∠BAC=100°,BD 平分∠ABC,求證:BD+AD=BC.

查看答案和解析>>
科目:初中數學 來源: 題型:
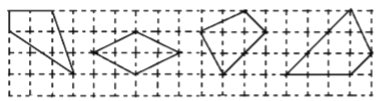
【題目】如圖所示,網格線是由邊長為1的小正方形格子組成的,小正方形的頂點叫做格點,以格點為頂點的多邊形叫做格點多邊形.小明與數學小組的同學研究發現,內部含有3個格點的四邊形的面積與該四邊形邊上的格點數有某種關系,請你觀察圖中的4個格點四邊形.設內部含有3個格點的四邊形的面積為![]() ,其各邊上格點的個數之和為
,其各邊上格點的個數之和為![]() ,則
,則![]() 與
與![]() 之間的關系式為__________.
之間的關系式為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
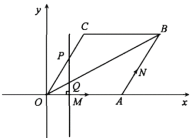
【題目】如圖,在直角坐標系XOY中,菱形OABC的邊OA在x軸正半軸上,點B,C在第一象限,∠C=120°,邊長OA=8,點M從原點O出發沿x軸正半軸以每秒1個單位長的速度作勻速運動,點N從A出發沿邊AB—BC—CO以每秒2個單位長的速度作勻速運動.過點M作直線MP垂直于x軸并交折線OCB于P,交對角線OB于Q,點M和點N同時出發,分別沿各自路線運動,點N運動到原點O時,M和N兩點同時停止運動.
(1)當t=2時,求線段PQ的長;
(2)求t為何值時,點P與N重合;
(3)設△APN的面積為S,求S與t的函數關系式及t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
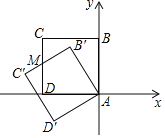
【題目】如圖,正方形ABCD的邊長為1,點A與原點重合,點B在y軸的正半軸上,點D在x軸的負半軸上,將正方形ABCD繞點A逆時針旋轉30°至正方形AB'C′D′的位置,B'C′與CD相交于點M,則點M的坐標為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BD為△ABC外接圓⊙O的直徑,且∠BAE=∠C.
(1)求證:AE與⊙O相切于點A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的長.
,求AD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個正整數能表示為兩個連續偶數的平方差,那么稱這個正整數為“神秘數”.如:4=22-02,12=42-22,20=62-42,因此4,12,20都是“神秘數”.
(1)試分析28是否為“神秘數”;
(2)下面是兩個同學演算后的發現,請選擇一個“發現”,判斷真、假,并說明理由.
①小能發現:兩個連續偶數2k+2和2k(其中k取非負整數)構造的“神秘數”也是4的倍數.
②小仁發現:2016是“神秘數”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD內接于圓O,連結BD,∠BAD=105°,∠DBC=75°.

(1)求證:BD=CD;
(2)若圓O的半徑為3,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com