
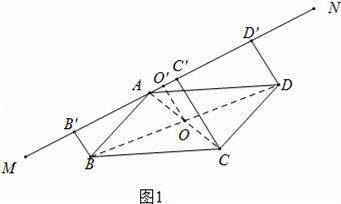
已知:如圖,直線MN經(jīng)過▱ABCD的頂點(diǎn)A,BB′⊥MN,CC′⊥MN,DD′⊥MN,B′、C′、D′是垂足.
(1)求證:CC′=BB′+DD′.
(2)現(xiàn)將直線MN向上或向下平移,請(qǐng)分別按下面要求畫出示意圖,寫出這時(shí)四條垂線段AA′、BB′、CC′、DD′之間的等量關(guān)系式.并簡(jiǎn)要說明證明思路.
(ⅰ)使點(diǎn)A、B、C、D都在直線MN的同一側(cè),這時(shí) ;
(ⅱ)使A點(diǎn)在MN的一側(cè),點(diǎn)B、C、D在另一側(cè),這時(shí) ;
(ⅲ)使點(diǎn)A、B在MN的一側(cè),點(diǎn)C、D在另一側(cè),這時(shí) .


【考點(diǎn)】平行四邊形的性質(zhì);全等三角形的判定與性質(zhì).
【分析】(1)如圖1中,連接AC、BD交于點(diǎn)O,作OO′⊥MN于O′,利用三角形中位線定理以及梯形中位線定理即可證明.
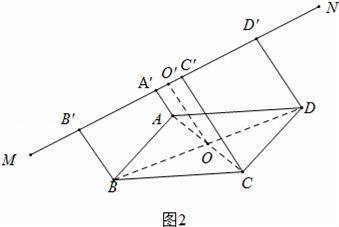
(2)(ⅰ)如圖2中,結(jié)論AA′+CC′=BB′+DD,連接AC、BD交于點(diǎn)O,作OO′⊥MN于OO′,利用梯形中位線定理可以證明AA′+CC′=BB′+DD.
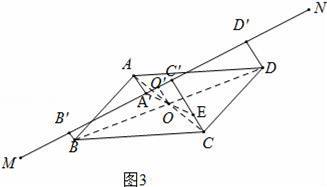
(ⅱ)如圖3中,結(jié)論CC′﹣AA′=BB′+DD,連接AC、BD交于點(diǎn)O,作OO′⊥MN于OO′,延長(zhǎng)A′O交CC′于E,只要證明CC′﹣AA′=2OO′.BB′+DD′=2OO′即可.
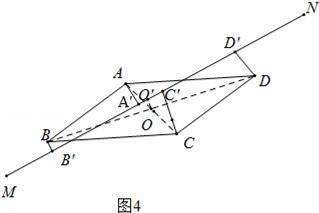
(ⅲ)如圖4中,結(jié)論CC′﹣AA′=DD′﹣BB,連接AC、BD交于點(diǎn)O,作OO′⊥MN于OO′,證明方法類似.
【解答】(1)證明:如圖1中,連接AC、BD交于點(diǎn)O,作OO′⊥MN于O′.
∵四邊形ABCD是平行四邊形,
∴AO=OC,BO=BD,
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,
∴BB′∥OO′∥CC′∥DD′,
∴B′O′=O′D′,AO′=O′C′,
∴CC′=2OO′,BB′+DD′=2OO′,
∴CC′=BB′+DD′.
(2)(ⅰ)當(dāng)點(diǎn)A、B、C、D都在直線MN的同一側(cè),
如圖2中,連接AC、BD交于點(diǎn)O,作OO′⊥MN于OO′,
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,AA′⊥MN,
∴BB′∥OO′∥CC′∥DD′∥AA′,
∴B′O′=O′D′,A′O′=O′C′,
∴AA′+CC′=2OO′,BB′+DD′=2OO′,
∴AA′+CC′=BB′+DD′,
故答案為AA′+CC′=BB′+DD′
(ⅱ)當(dāng)A點(diǎn)在MN的一側(cè),點(diǎn)B、C、D在另一側(cè),如圖3中,
如圖3中,連接AC、BD交于點(diǎn)O,作OO′⊥MN于OO′,延長(zhǎng)A′O交CC′于E.
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,AA′⊥MN,
∴BB′∥OO′∥CC′∥DD′∥AA′,
∴B′O′=O′D′,A′O′=O′C′,
∴BB′+DD′=2OO′,
∵AA′∥CE,
∴∠AA′O=∠OEC
 ,
,
在△AA′O和△CEO中,
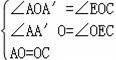
 ,
,
∴△AA′O≌△CEO,
∴AA′=EC,A′O=OE,
∴EC′=2OO′,即CC′﹣AA′=2OO′,
∴CC′﹣AA′=BB′+DD′,
故答案為CC′﹣AA′=BB′+DD.
(ⅲ)當(dāng)點(diǎn)A、B在MN的一側(cè),點(diǎn)C、D在另一側(cè),
如圖4中,連接AC、BD交于點(diǎn)O,作OO′⊥MN于OO′,
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,AA′⊥MN,
∴BB′∥OO′∥CC′∥DD′∥AA′,
∴B′O′=O′D′,A′O′=O′C′,
同理可以證明:CC′﹣AA′=2OO′,DD′﹣BB′=2OO′,
∴CC′﹣AA′=DD′﹣BB′,
故答案為CC′﹣AA′=DD′﹣BB′.




【點(diǎn)評(píng)】本題考查平行四邊形的性質(zhì)、三角形的中位線定理、梯形的中位線定理、全等三角形的判定和性質(zhì),解題的關(guān)鍵是正確添加輔助線,利用中位線定理解決問題,題目有點(diǎn)難度,學(xué)會(huì)轉(zhuǎn)化的思想,把問題轉(zhuǎn)化為三角形中位線、梯形中位線解決.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
如圖,OP=1,過P作PP1⊥OP且PP1=1,得OP1= ;再過P1作P1P2⊥OP1且P1P2=1,得OP2=
;再過P1作P1P2⊥OP1且P1P2=1,得OP2= ;又過P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法繼續(xù)作下去,得
;又過P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法繼續(xù)作下去,得 = .
= .

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
為了解某校學(xué)生每日運(yùn)動(dòng)量,收集數(shù)據(jù)正確的是( )
A.調(diào)查該校七年級(jí)學(xué)生每日運(yùn)動(dòng)量;
B.調(diào)查該校女生每日的運(yùn)動(dòng)量
C.調(diào)查該校男生每日的運(yùn)動(dòng)量;
D.從七、八、九年級(jí)各抽調(diào)100人調(diào)查他們每日的運(yùn)動(dòng)量
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
下列各組長(zhǎng)度的線段能組成直角三角形的是( )
A.a=2,b=3,c=4 B.a=4,b=4,c=5
C.a=5,b=6,c=7 D.a=5,b=12,c=13
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
某養(yǎng)魚專業(yè)戶年初在魚塘中投放了500條草魚苗,6個(gè)月后從中隨機(jī)撈取17條草魚,稱重如下:
| 草魚質(zhì)量(單位:千克) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
| 草魚數(shù)量(單位:條) | 2 | 3 | 2 | 3 | 4 | 1 | 1 |
|
 估計(jì)這魚塘中年初投放的500條草魚此時(shí)的總質(zhì)量大約為多少千克( )
估計(jì)這魚塘中年初投放的500條草魚此時(shí)的總質(zhì)量大約為多少千克( )
A.845 B.854 C.846 D.847
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
為了解本科生的就業(yè)狀況,今年3月,某網(wǎng)站對(duì)本科生的簽約狀況進(jìn)行了網(wǎng)絡(luò)調(diào)查.截止3月底,參與網(wǎng)絡(luò)調(diào)查的12000人中,只有4320人已與用人單位簽約.在這個(gè)網(wǎng)絡(luò)調(diào)查中,樣本容量是____________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
油箱中有油20升,油從管道中勻速流出,100分鐘流完.油箱中剩油量 (升)與流出的時(shí)間
(升)與流出的時(shí)間 (分)間的函數(shù)關(guān)系式是( )
(分)間的函數(shù)關(guān)系式是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
為了研究某的高度h(千米)與溫度t(℃)之間的關(guān)系,某日研究人員在該地的不同高度處同時(shí)進(jìn)行了若干次實(shí)驗(yàn),測(cè)得的數(shù)據(jù)如下表:
| h/千米 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
| t/℃ | 23 | 21 | 19 | 17 | 15 | 13 | 11 | … |
(1)在直角坐標(biāo)系中,作出各組有序數(shù)對(duì)(h,t)所對(duì)應(yīng)的點(diǎn).
(2)這些點(diǎn)是否近似在一條直線上?
(3)估計(jì)此時(shí)3.5千米高度處的溫度.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com