
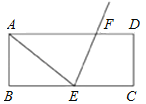
【題目】如圖,長方形ABCD中,E為BC中點,作∠AEC的角平分線交AD于F點.若AB=6,AD=16,則FD的長度為何?( )
A.4 B.5 C.6 D.8
【答案】C
【解析】
試題分析:首先由矩形ABCD的性質,得BC=AD=16,已知E為BC中點,則BE=BC÷2=8,根據勾股定理在直角三角形ABE中可求出AE,再由∠AEC的角平分線交AD于F點,得∠AEF=∠CEF,已知矩形ABCD,AD∥BC,
則∠AFE=∠CEF,所以∠AEF=∠AFE,所以AF=AE,從而求出FD.
解:已知矩形ABCD,∴BC=AD=16,
又E為BC中點,
∴BE=![]() ×BC=
×BC=![]() ×16=8,
×16=8,
在直角三角形ABE中,
AE2=AB2+BE2=62+82=100,
∴AE=10,
已知矩形ABCD,
∴AD∥BC,
∴∠AFE=∠CEF,
又∠AEC的角平分線交AD于F點,
∴∠AEF=∠CEF,
∴∠AEF=∠AFE,
∴AF=AE=10,
∴FD=AD﹣AF=16﹣10=6,
故選:C.


科目:初中數學 來源: 題型:
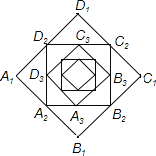
【題目】如圖,小宋作出了邊長為2的第一個正方形A1B1C1D1,算出了它的面積.然后分別取正方形A1B1C1D1四邊的中點A2、B2、C2、D2作出了第二個正方形A2B2C2D2,算出了它的面積.用同樣的方法,作出了第三個正方形A3B3C3D3,算出了它的面積…,由此可得,第六個正方形A6B6C6D6的面積是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程2x2+(a+4)x+a=0.
(1)求證:無論a為任何實數,此方程總有兩個不相等的實數根;
(2)拋物線![]() 與x軸的一個交點的橫坐標為
與x軸的一個交點的橫坐標為![]() ,其中a≠0,將拋物線C1向右平移
,其中a≠0,將拋物線C1向右平移![]() 個單位,再向上平移
個單位,再向上平移![]() 個單位,得到拋物線C2.求拋物線C2的解析式;
個單位,得到拋物線C2.求拋物線C2的解析式;
(3)點A(m,n)和B(n,m)都在(2)中拋物線C2上,且A、B兩點不重合,求代數式2m3﹣2mn+2n3的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“石頭、剪刀、布”是民間廣為流傳的游戲,游戲時,雙方每次只能做“石頭”、“剪刀”、“布”這三種手勢中的一種.假定雙方每次都是等可能的做這三種手勢.
問:小強和小剛在一次游戲時,
(1)兩個人同時出現“石頭”手勢的概率是多少?
(2)兩個人出現不同手勢的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市一月份的營業額為200萬元,已知第一季度的總營業額共1000萬元,如果平均每月增長率為x,則由題意列方程應為( )
A.200(1+x)2=1000
B.200+200×2x=1000
C.200+200×3x=1000
D.200[1+(1+x)+(1+x)2]=1000
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com