
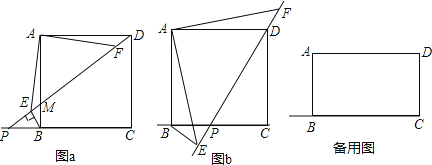
【題目】如圖,正方形ABCD,點P在射線CB上運動(不包含點B、C),連接DP,交AB于點M,作BE⊥DP于點E,連接AE,作∠FAD=∠EAB,FA交DP于點F.
(1)如圖a,當點P在CB的延長線上時,
①求證:DF=BE;
②請判斷DE、BE、AE之間的數量關系并證明;
(2)如圖b,當點P在線段BC上時,DE、BE、AE之間有怎樣的數量關系?請直接寫出答案,不必證明;
(3)如果將已知中的正方形ABCD換成矩形ABCD,且AD:AB=![]() :1,其他條件不變,當點P在射線CB上時,DE、BE、AE之間又有怎樣的數量關系?請直接寫出答案,不必證明.
:1,其他條件不變,當點P在射線CB上時,DE、BE、AE之間又有怎樣的數量關系?請直接寫出答案,不必證明.
【答案】(1)詳見解析;②DE=BE+![]() AE,理由詳見解析;(2)DE=
AE,理由詳見解析;(2)DE=![]() AE﹣BE;(3)DE=2AE+
AE﹣BE;(3)DE=2AE+![]() BE或DE=2AE﹣
BE或DE=2AE﹣![]() BE.
BE.
【解析】
(1)①由正方形的性質得到AD=AB,∠BAD=90°,判斷出△ABE≌△ADF,即可;②由①得到△ABE≌△ADF,并且判斷出△EAF為直角三角形,用勾股定理即可;
(2)先由正方形的性質和已知條件判斷出△ABE≌△ADF,再用判斷出△EAF為直角三角形,用勾股定理即可;
(3)分兩種情況討論,先由正方形的性質和已知條件判斷出△ABE∽△ADF,AF=![]() AE,DF=
AE,DF=![]() BE,再判斷出△EAF為直角三角形,用勾股定理結合圖形可得結論.
BE,再判斷出△EAF為直角三角形,用勾股定理結合圖形可得結論.
證明:(1)①正方形ABCD中,AD=AB,∠ADM+∠AMD=90°
∵BE⊥DP,
∴∠EBM+∠BME=90°,
∵∠AMD=∠BME,
∴∠EBM=∠ADM,
在△ABE和△ADF中,
 ,
,
∴△ABE≌△ADF,
∴DF=BE;
②DE=BE+![]() AE,
AE,
理由:由(1)有△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∴∠BAE+∠FAM=∠DAF+∠FAM,
∴∠EAF=∠BAD=90°,
∴EF=![]() AE,
AE,
∵DE=DF+EF,
∴DE=BE+![]() AE;
AE;
(2)DE=![]() AE﹣BE;
AE﹣BE;
理由:正方形ABCD中,AD=AB,∠BAD=∠BAE+∠DAE=90°,
∵∠FAD=∠EAB,
∴∠EAF=∠BAD=90°,
∴∠AFE+∠AEF=90°
∵BE⊥DP,
∴∠BEA+∠AEF=90°,
∴∠BEA=∠AFE,
∵∠FAD=∠EAB,AD=AB
∴△ABE≌△ADF,
∴AE=AF,BE=DF
∵∠EAF=90°
∴EF=![]() AE,
AE,
∵EF=DF+DE=![]() AE,
AE,
∴DE=![]() AE﹣DF=
AE﹣DF=![]() AE﹣BE;
AE﹣BE;
(3)DE=2AE+![]() BE或DE=2AE﹣
BE或DE=2AE﹣![]() BE.
BE.
①如圖1所示時,
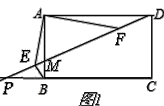
正方形ABCD中,∠ADM+∠AMD=90°
∵BE⊥DP,
∴∠EBM+∠BME=90°,
∵∠AMD=∠BME,
∴∠EBM=∠ADM,
∵∠FAD=∠EAB
∴△ABE∽△ADF,
∴![]() ,
,
∵AD:AB=![]() :1,
:1,
∴![]() ,
,
∴AF=![]() AE,DF=
AE,DF=![]() BE
BE
∵∠FAD=∠EAB
∴∠EAF=∠EAB+∠BAF=∠FAD+∠BAF=∠BAD=90°,
∴EF=![]() =2AE=DE﹣DF=DE﹣
=2AE=DE﹣DF=DE﹣![]() BE,
BE,
即:DE=2AE+![]() BE;
BE;
②如圖2所示,
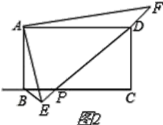
∵∠DAF=∠BAE,
∴∠EAF=∠BAD=90°,
∵∠DAF=∠BAE,
∴△BAE∽△DAF,
∴![]() ,
,
∵AD:AB=![]() :1,
:1,
∴![]() ,
,
∴AF=![]() AE,DF=
AE,DF=![]() BE,
BE,
∵∠EAF=90°,
根據勾股定理得,EF=![]() =2AE=DE+DF=DE+
=2AE=DE+DF=DE+![]() BE,
BE,
∴DE=2AE﹣![]() BE.
BE.


科目:初中數學 來源: 題型:
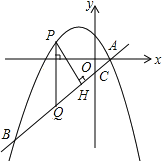
【題目】如圖,在平面直角坐標系中,直線y=![]() 與拋物線y=
與拋物線y=![]() 交于A、B兩點,且點A在x軸上,點B的橫坐標為-4,點P為直線AB上方的拋物線上一動點(不與點A、B重合),過點P作x軸的垂線交直線AB于點Q,PH⊥AB于H.
交于A、B兩點,且點A在x軸上,點B的橫坐標為-4,點P為直線AB上方的拋物線上一動點(不與點A、B重合),過點P作x軸的垂線交直線AB于點Q,PH⊥AB于H.
(1)求b的值及sin∠PQH的值;
(2)設點P的橫坐標為t,用含t的代數式表示點P到直線AB的距離PH的長,并求出PH之長的最大值以及此時t的值;
(3)連接PB,若線段PQ把△PBH分成成△PQB與△PQH的面積相等,求此時點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
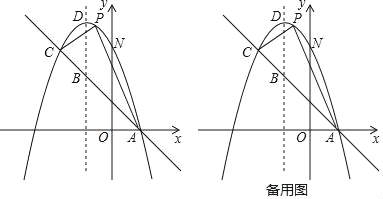
【題目】如圖,已知拋物線y=﹣x2+bx+c與一直線相交于A(1,0)、C(﹣2,3)兩點,與y軸交于點N,其頂點為D.
(1)求拋物線及直線AC的函數關系式;
(2)若P是拋物線上位于直線AC上方的一個動點,求△APC的面積的最大值及此時點P的坐標;
(3)在對稱軸上是否存在一點M,使△ANM的周長最小.若存在,請求出M點的坐標和△ANM周長的最小值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形紙片ABCD沿對角線BD折疊,使點A落在平面上的F點處,DF交BC于點E.
(1)求證:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,E為矩形ABCD的邊AD上一點,點P從點B出發沿折線BE-ED-DC運動到點C停止,點Q從點B出發沿BC運動到點C停止,它們運動的速度都是1cm/s.若點P、點Q同時開始運動,設運動時間為t(s),△BPQ的面積為y(![]() ),已知y與t之間的函數圖象如圖2所示.
),已知y與t之間的函數圖象如圖2所示.

給出下列結論:①當0<t≤10時,△BPQ是等腰三角形;②![]() =48
=48![]() ;③當14<t<22時,y=110-5t;④在運動過程中,使得△ABP是等腰三角形的P點一共有3個;⑤△BPQ與△ABE相似時,t=14.5.
;③當14<t<22時,y=110-5t;④在運動過程中,使得△ABP是等腰三角形的P點一共有3個;⑤△BPQ與△ABE相似時,t=14.5.
其中正確結論的序號是_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學九(1)班為了了解全班學生喜歡球類活動的情況,采取全面調查的方法,從足球、乒乓球、籃球、排球等四個方面調查了全班學生的興趣愛好,根據調查的結果組建了4個興趣小組,并繪制成如圖所示的兩幅不完整的統計圖(如圖①,②,要求每位學生只能選擇一種自己喜歡的球類),請你根據圖中提供的信息解答下列問題:
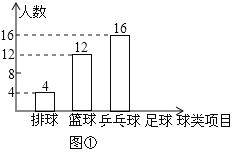

(1)九(1)班的學生人數為 ,并把條形統計圖補充完整;
(2)扇形統計圖中m= ,n= ,表示“足球”的扇形的圓心角是 度;
(3)排球興趣小組4名學生中有3男1女,現在打算從中隨機選出2名學生參加學校的排球隊,請用列表或畫樹狀圖的方法求選出的2名學生恰好是1男1女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某一天,水果經營戶老張用1600元從水果批發市場批發獼猴桃和芒果共50千克,后再到水果市場去賣,已知獼猴桃和芒果當天的批發價和零售價如表所示:
品名 | 獼猴桃 | 芒果 |
批發價 | 20 | 40 |
零售價 | 26 | 50 |
![]() 他購進的獼猴桃和芒果各多少千克?
他購進的獼猴桃和芒果各多少千克?
![]() 如果獼猴桃和芒果全部賣完,他能賺多少錢?
如果獼猴桃和芒果全部賣完,他能賺多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,菱形ABCD在第一象限內,邊BC與x軸平行,A、B兩點的縱坐標分別為3,1,反比例函數y=![]() 的圖象經過A,B兩點,則點D的坐標為( )
的圖象經過A,B兩點,則點D的坐標為( )
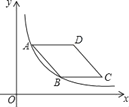
A. (2![]() ﹣1,3)B. (2
﹣1,3)B. (2![]() +1,3)
+1,3)
C. (2![]() ﹣1,3)D. (2
﹣1,3)D. (2![]() +1,3)
+1,3)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com