
 ,連結AE,CE.延長CE到F,連結BF,使得BC=BF.若AB=1,則下列結論:①AE=CE; ②F到BC的距離為
,連結AE,CE.延長CE到F,連結BF,使得BC=BF.若AB=1,則下列結論:①AE=CE; ②F到BC的距離為 ;③BE+EC=EF;④
;③BE+EC=EF;④ ;⑤
;⑤ .其中正確的個數是
.其中正確的個數是
| A.2個 | B.3個 | C.4個 | D.5個 |

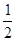 BF=
BF=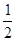 ,∴②錯誤;
,∴②錯誤;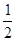 ,BF=1,
,BF=1,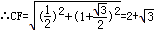
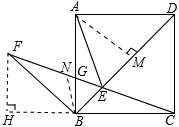
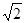 ,
,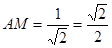
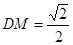 ,
,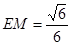
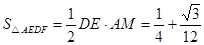 ,∴④錯誤;
,∴④錯誤;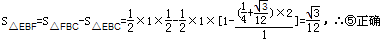


科目:初中數學 來源:不詳 題型:解答題
 (如圖2).這時AB與
(如圖2).這時AB與 相交于點O,與
相交于點O,與 相交于點F.
相交于點F.
 = °;
= °; 的內切圓半徑;
的內切圓半徑; 繞著點C逆時針再旋轉
繞著點C逆時針再旋轉 度(
度( )得△
)得△ ,若△
,若△ 為等腰三角形,求
為等腰三角形,求 的度數(精確到0.1°).
的度數(精確到0.1°).查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
 ,AC、BD相交于點O,
,AC、BD相交于點O, 交AD于點E,則△ABE的周長為( )
交AD于點E,則△ABE的周長為( )
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com