
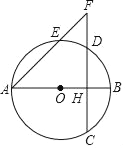
【題目】如圖,已知AB是圓O的直徑,弦CD⊥AB,垂足H在半徑OB上,AH=5,CD=![]() ,點E在弧AD上,射線AE與CD的延長線交于點F.
,點E在弧AD上,射線AE與CD的延長線交于點F.
(1)求圓O的半徑;
(2)如果AE=6,求EF的長.
【答案】(1) 圓的半徑為4.5;(2) EF=![]() .
.
【解析】
(1)連接OD,根據垂徑定理得:DH=2![]() ,設圓O的半徑為r,根據勾股定理列方程可得結論;
,設圓O的半徑為r,根據勾股定理列方程可得結論;
(2)過O作OG⊥AE于G,證明△AGO∽△AHF,列比例式可得AF的長,從而得EF的長.
(1)連接OD,
∵直徑AB⊥弦CD,CD=4![]() ,
,
∴DH=CH=![]() CD=2
CD=2![]() ,
,
在Rt△ODH中,AH=5,
設圓O的半徑為r,
根據勾股定理得:OD2=(AH﹣OA)2+DH2,即r2=(5﹣r)2+20,
解得:r=4.5,
則圓的半徑為4.5;
(2)過O作OG⊥AE于G,
∴AG=![]() AE=
AE=![]() ×6=3,
×6=3,
∵∠A=∠A,∠AGO=∠AHF,
∴△AGO∽△AHF,
∴![]() ,
,
∴![]() ,
,
∴AF=![]() ,
,
∴EF=AF﹣AE=![]() ﹣6=
﹣6=![]() .
.


科目:初中數學 來源: 題型:
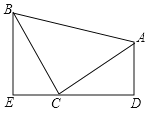
【題目】如圖,平行四邊形ABCD中,AE平分∠BAD,交BC于點E,且AB=AE,延長AB與DE的延長線交于點F.下列結論中:①△ABC≌△AED;②△ABE是等邊三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正確的是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)模型建立:
如圖,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直線
,直線![]() 經過點
經過點![]() ,過
,過![]() 作
作![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() .求證:
.求證:![]() ;
;
(2)模型應用:
①如圖,一次函數![]() 的圖象分別與
的圖象分別與![]() 軸、
軸、![]() 軸交于點
軸交于點![]() 、
、![]() ,以線段
,以線段![]() 為腰在第一象限內作等腰直角三角形
為腰在第一象限內作等腰直角三角形![]() ,則
,則![]() 點的坐標為___________(直接寫出結果)
點的坐標為___________(直接寫出結果)
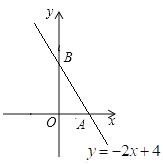
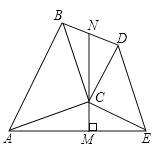
②如圖,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,連接
,連接![]() 、
、![]() ,作
,作![]() 于
于![]() 點,延長
點,延長![]() 與
與![]() 交于點
交于點![]() ,求證:
,求證:![]() 是
是![]() 的中點.
的中點.
查看答案和解析>>
科目:初中數學 來源: 題型:
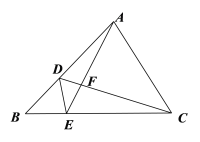
【題目】已知:如圖,在△ABC中,點D,E分別在邊AB,BC上,BABD=BCBE
(1)求證:△BDE∽△BCA;
(2)如果AE=AC,求證:AC2=ADAB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表中給出了變量x,與y=ax2,y=ax2+bx+c之間的部分對應值,(表格中的符號“…”表示該項數據已丟失)
x | ﹣1 | 0 | 1 |
ax2 | … | … | 1 |
ax2+bx+c | 7 | 2 | … |
(1)求拋物線y=ax2+bx+c的表達式
(2)拋物線y=ax2+bx+c的頂點為D,與y軸的交點為A,點M是拋物線對稱軸上一點,直線AM交對稱軸右側的拋物線于點B,當△ADM與△BDM的面積比為2:3時,求B點坐標;
(3)在(2)的條件下,設線段BD與x軸交于點C,試寫出∠BAD和∠DCO的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
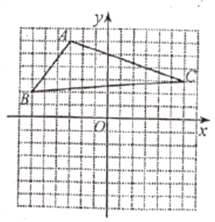
【題目】如圖,![]() 的三個頂點的坐標分別為
的三個頂點的坐標分別為![]() 、
、![]() 、
、![]() .
. ![]() 與
與![]() 關于
關于![]() 軸對稱,
軸對稱,![]() 與
與![]() 關于
關于![]() 軸對稱,點
軸對稱,點![]() 、
、![]() 、
、![]() 分別是點
分別是點![]() 、
、![]() 、
、![]() 的對應點,點
的對應點,點![]() 、
、![]() 、
、![]() 分別是
分別是![]() 、
、![]() 、
、![]() 的對應點.
的對應點.
(1)畫出![]() 與
與![]() ,并寫出點
,并寫出點![]() 、
、![]() 、
、![]() 的坐標;
的坐標;
(2)連接![]() 、
、![]() ,求六邊形
,求六邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,在邊
,在邊![]() 上順次取點
上順次取點![]() ,
,![]() ,
,![]() …,在邊
…,在邊![]() 上順次取點
上順次取點![]() ,
,![]() ,
,![]() …,使得
…,使得![]() …,得到等腰△
…,得到等腰△![]() ,△
,△![]() ,△
,△![]() ,△
,△![]() …
…

(1)若![]() =30°,可以得到的最后一個等腰三角形是_________;
=30°,可以得到的最后一個等腰三角形是_________;
(2)若按照上述方式操作,得到的最后一個等腰三角形是△![]() ,則
,則![]() 的度數
的度數![]() 的取值范圍是________.
的取值范圍是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AC是⊙O的直徑,點B,D在⊙O上,點E在⊙O外,∠EAB=∠D=30°.
(1)∠C的度數為 ;
(2)求證:AE是⊙O的切線;
(3)當AB=3時,求圖中陰影部分的面積(結果保留根號和π).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com