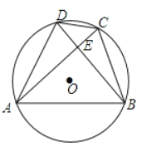
【題目】如圖，四邊形
內接于⊙
，
，
，垂足為
．
(1)若
，則
°．
(2)求證: 
；
(3)若
，
，求
的值．
【答案】（1）110；（2）見解析；（3）
【解析】
（1）由等腰三角形的性質求出∠ABC和∠ACB的度數，然后根據圓內接四邊形的性質即可求出∠ADC的值；
（2）設
，由等腰三角形的性質求表示出∠ABC和∠ACB，進而得出∠CBD，由圓周角定理得出∠DAC=∠CBD=
，即可得出結論；
（3）由△ECD∽△EBA，可得BE=2CE，設CE=x，則BE=2x，AE=10-x，
在Rt△ABE中，求出x的值，再在Rt△BCE中即可求出BC的值．
解：（1）∵AB=AC，
，
∴∠ABC=∠ACB=70°，
∵四邊形
內接于⊙
，
∴∠ADC=180°-70°=110°；
（2）設，
∵AB=AC，
∴∠ABC=∠ACB=
，
∵BD⊥AC，
∴∠AEB=∠BEC=90°，
∴∠CBD=90°-=，
∵∠DAC=∠CBD，
∴
；，
（3）∵∠ACD=∠ABD，∠BDC=∠BAC，
∴△ECD∽△EBA，
∴
.
∵
，
，
∴
，
∴BE=2CE，
設CE=x，則BE=2x，AE=10-x，
在Rt△ABE中，
(10-x)2+(2x)2=102，
解得
x1=4，x2=0（舍去），
∴CE=4，BE=8，
∴BC=
=．
舉一反三期末百分沖刺卷系列答案科目：初中數學 來源： 題型：
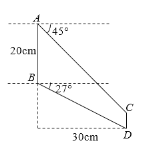
【題目】某校航模小組打算制作模型飛機，設計了如圖所示的模型飛機機翼圖紙．圖紙中AB∥CD，均與水平方向垂直，機翼前緣AC、機翼后緣BD與水平方向形成的夾角度數分別為45°、27°，AB＝20cm，點D到直線AB的距離為30cm．求機翼外緣CD的長度．（參考數據：sin27°≈0.45，cos27°≈0.89，tan27°≈0.51．）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知等腰Rt△ABC和等腰Rt△AED中，∠ACB=∠AED=90°，且AD=AC．
（1）發現：如圖1，當點E在AB上且點C和點D重合時，若點M、N分別是DB、EC的中點，則MN與EC的位置關系是 ，MN與EC的數量關系是 ．
（2）探究：若把（1）小題中的△AED繞點A順時針旋轉45°得到的圖2，連接BD和EC，并連接DB、EC的中點M、N，則MN與EC的位置關系和數量關系仍然能成立嗎？若成立，請給予證明，若不成立，請說明理由．
（3）若把（1）小題中的△AED繞點A逆時針旋轉45°得到的圖3，連接BD和EC，并連接DB、EC的中點M、N，則MN與EC的位置關系和數量關系仍然能成立嗎？若成立，請給予證明，若不成立，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，樓房BD的前方豎立著旗桿AC．小亮在B處觀察旗桿頂端C的仰角為45°，在D處觀察旗桿頂端C的俯角為30°，樓高BD為20米．
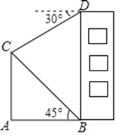
（1）求∠BCD的度數；
（2）求旗桿AC的高度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有四張正面分別標有數字0，1，2，3的不透明卡片，它們除數字外其余全部相同，現將它們背面朝上洗均勻．
(1)隨機抽出一張卡片，則抽到數字“2”的概率為 ;
(2)隨機抽出一張卡片，記下數字后放回并攪勻，再隨機抽出一張卡片，請用列表或畫樹狀圖的方法，求兩次抽出的卡片上的數字之和是3的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如今很多初中生購買飲品飲用，既影響身體健康又給家庭增加不必要的開銷，為此數學興趣小組對本班同學一天飲用飲品的情況進行了調查，大致可分為四種：
A：自帶白開水；B：瓶裝礦泉水；C：碳酸飲料；D：非碳酸飲料．
根據統計結果繪制如下兩個統計圖（如圖），根據統計圖提供的信息，解答下列問題：
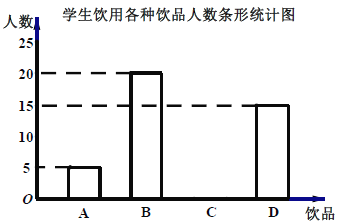
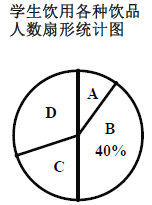
（1）請你補全條形統計圖；
（2）在扇形統計圖中，求“碳酸飲料”所在的扇形的圓心角的度數；
（3）為了養成良好的生活習慣，班主任決定在自帶白開水的5名同學（男生2人，女生3人）中隨機抽取2名同學擔任生活監督員，請用列表法或樹狀圖法求出恰好抽到一男一女的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】中國的數字支付正在引領未來世界的支付方式變革．某校數學興趣小組設計了一份調查問卷，要求每人選且只選一種你最喜歡的支付方式．現將調查結果進行統計并繪制成如下兩幅不完整的統計圖，請結合圖中所給的信息解答下列問題：
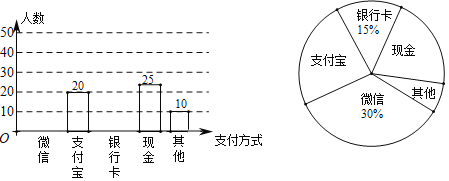
（1）這次活動共調查了 人；在扇形統計圖中，表示“支付寶”支付的扇形圓心角的度數為 ；
（2）將條形統計圖補充完整．觀察此圖，將各種支付方式調查人數組成一組數據，求這組數據的“中位數”是“ ”；
（3）在一次購物中，小明和小亮都想從“微信”、“支付寶”、“銀行卡”三種支付方式中選一種方式進行支付，請用畫樹狀圖或列表的方法，求兩人選同種支付方式的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商店經銷一種雙肩包，已知這種雙肩包的成本價為每個30元．市場調查發現，這種雙肩包每天的銷售量y（單位:個）與銷售單價x（單位:元）有如下關系：y=－x+60（30≤x≤60）．
設這種雙肩包每天的銷售利潤為w元．
（1）求w與x之間的函數解析式；
（2）這種雙肩包銷售單價定為多少元時，每天的銷售利潤最大？最大利潤是多少元？
（3）如果物價部門規定這種雙肩包的銷售單價不高于48元，該商店銷售這種雙肩包每天要獲得200元的銷售利潤，銷售單價應定為多少元？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
