
【題目】已知反比例函數的圖![]() 象與一次函數y2=ax+b的圖象交于點A(1,4)和點B(m,﹣2),
象與一次函數y2=ax+b的圖象交于點A(1,4)和點B(m,﹣2),
(1)求這兩個函數的關系式;
(2)觀察圖象,寫出使得y1>y2成立的自變量x的取值范圍;
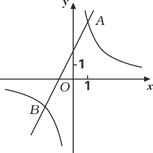
【答案】(1)![]() ,y2=2x+2.(2)x<﹣2 或0<x<1.
,y2=2x+2.(2)x<﹣2 或0<x<1.
【解析】試題分析:(1)將點A坐標代入y1=![]() 中,得以k的值,即可得到反比例函數的解析式,將點B坐標代入反比比例函數的解析式中即可求出m的值,再將A、B兩點坐標代入y2=ax+b中,從而求出a、b的值,即為一次函數的解析式;
中,得以k的值,即可得到反比例函數的解析式,將點B坐標代入反比比例函數的解析式中即可求出m的值,再將A、B兩點坐標代入y2=ax+b中,從而求出a、b的值,即為一次函數的解析式;
(2)由y1>y2,即寫出反比例函數圖像在一次函數圖像上方時對應自變量x的取值范圍即可;
試題解析:
(1)∵函數y1=![]() 的圖象過點A(1,4),即k=4,
的圖象過點A(1,4),即k=4,
∴k=4,即y1=4/x,
又∵點B(m,﹣2)在y1上,
∴m=﹣2,∴B(﹣2,﹣2),
又∵一次函數y2=ax+b過A、B兩點,
即 ![]() ,解之得
,解之得![]() .
.
∴y2=2x+2.
(2)要使y1>y2,即函數y1的圖象總在函數y2的圖象上方,
∴x<﹣2 或0<x<1.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:初中數學 來源: 題型:
【題目】在一個口袋里有四個完全相同的小球,把它們分別標號為1,2,3,4,小明和小強采取的摸取方法分別是:
小明:隨機摸取一個小球記下標號,然后放回,再隨機摸取一個小球,記下標號;
小強:隨機摸取一個小球記下標號,不放回,再隨機摸取一個小球,記下標號.
(1)用畫樹狀圖(或列表法)分別表示小明和小強摸球的所有可能出現的結果;
(2)分別求出小明和小強兩次摸球的標號之和等于5的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某隧道口的橫截面是拋物線形,已知路寬AB為6米,最高點離地面的距離OC為5米.以最高點O為坐標原點,拋物線的對稱軸為y軸,1米為數軸的單位長度,建立平面直角坐標系,求:(1)以這一部分拋物線為圖象的函數解析式,并寫出x的取值范圍;(2)有一輛寬2.8米,高1米的農用貨車(貨物最高處與地面AB的距離)能否通過此隧道?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一段拋物線y=-x(x-3)(0≤x≤3),記為C1,它與x軸交于點O,A1;將C1繞點A1旋轉180°得C2,交x 軸于點A2;將C2繞點A2旋轉180°得C3,交x 軸于點A3;……如此進行下去,得到一條“波浪線”.若點P(37,m)在此“波浪線”上,則m的值為______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com