
已知四邊形ABCD是正方形,O為正方形對(duì)角線的交點(diǎn),一動(dòng)點(diǎn)P從B開(kāi)始,沿射線BC運(yùn)動(dòng),連結(jié)DP,作CN⊥DP于點(diǎn)M,且交直線AB于點(diǎn)N,連結(jié)OP,ON。(當(dāng)P在線段BC上時(shí),如圖1:當(dāng)P在BC的延長(zhǎng)線上時(shí),如圖2)
(1)請(qǐng)從圖1,圖2中任選一圖證明下面結(jié)論:
①BN=CP: ②OP=ON,且OP⊥ON
(2) 設(shè)AB=4,BP=x,試確定以O(shè)、P、B、N為頂點(diǎn)的四邊形的面積y與x的函數(shù)關(guān)系。

(1)證明:如圖1,
①∵四邊形ABCD是正方形,
∴OC=OB,DC=BC,∠DCB=∠CBA=90°,∠OCB=∠OBA=45°,∠DOC=90°,DC∥AB。
∵DP⊥CN,∴∠CMD=∠DOC=90°。
∴∠BCN+∠CPD=90°,∠PCN+∠DCN=90°。∴∠CPD=∠CNB。
∵DC∥AB,∴∠DCN=∠CNB=∠CPD。
∵在△DCP和△CBN中,∠DCP=∠CBN,∠CPD=∠BNC,DC=BC,
∴△DCP≌△CBN(AAS)。∴CP=BN。
②∵在△OBN和△OCP中,OB=OC,∠OCP=∠OBN, CP=BN ,
∴△OBN≌△OCP(SAS)。∴ON=OP,∠BON=∠COP。
∴∠BON+∠BOP=∠COP+∠BOP,即∠NOP=∠BOC=90°。
∴ON⊥OP。
(2)解:∵AB=4,四邊形ABCD是正方形,∴O到BC邊的距離是2。
圖1中, ,
,
圖2中,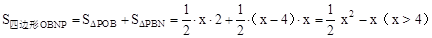 。
。
∴以O(shè)、P、B、N為頂點(diǎn)的四邊形的面積y與x的函數(shù)關(guān)系是:
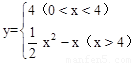 。
。
【解析】正方形的性質(zhì),三角形外角性質(zhì),全等三角形的判定和性質(zhì),兩線垂直的判定,多邊形的面積的分解,函數(shù)解析式的確定,分段函數(shù),點(diǎn)到直線的距離。
【分析】(1)對(duì)于圖1,證明線段相等,一般情況下找全等。根據(jù)BN,CP的分布情況 可以觀察△CNB和△DPC,然后證明兩三角形全等。也可以觀察△CAN和△DBP,證明AN=BP,從而有BN=CP。
對(duì)于圖2,證明如下:
①∵ABCD為正方形,AC,BD為對(duì)角線,∴∠DCP=90º。
∵CM⊥DP, ∴∠PCM=∠PDC。∴∠PDB=∠CAN。
又∵∠DPB=∠ANC,BD=AC,∴△PDB≌△NCA(ASA)。
∴PB=AN,DP=CN。∴CP=BN。
②∵∠PDB=∠CAN,OD=OC, CP=BN,∴△PDO≌△NCO(SAS)。
∴OP=ON,∠DOP=∠CON。
∵∠DOC=90º,∴∠PON=∠NOC+POC=∠DOP+∠POC=∠DOC=90º。∴OP⊥ON。
(2)求以O(shè)、P、B、N為頂點(diǎn)的四邊形的面積,則要把四邊形分解為兩個(gè)三角形去解決問(wèn)題。圖1中,S四邊形OPBN=S△OBN+S△BOP,,;圖2中,S四邊形OBNP=S△POB+S△PBN,代入求出即可。


 培優(yōu)口算題卡系列答案
培優(yōu)口算題卡系列答案 開(kāi)心口算題卡系列答案
開(kāi)心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:

查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com