
【題目】如圖,矩形的邊OA在x軸上,邊OC在y軸上,點B的坐標為(10,8),沿直線OD折疊矩形,使點A正好落在BC上的E處,E點坐標為(6,8),拋物線y=ax2+bx+c經過O、A、E三點.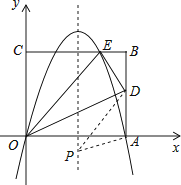
(1)求此拋物線的解析式;
(2)求AD的長;
(3)點P是拋物線對稱軸上的一動點,當△PAD的周長最小時,求點P的坐標.
【答案】
(1)
解:∵四邊形ABCD是矩形,B(10,8),
∴A(10,0),
又拋物線經過A、E、O三點,把點的坐標代入拋物線解析式可得
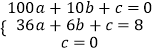 ,解得
,解得 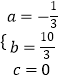 ,
,
∴拋物線的解析式為y=﹣ ![]() x2+
x2+ ![]() x
x
(2)
解:由題意可知:AD=DE,BE=10﹣6=4,AB=8,
設AD=x,則ED=x,BD=AB﹣AD=8﹣x,
在Rt△BDE中,由勾股定理可知ED2=EB2+BD2,即x2=42+(8﹣x)2,解得x=5,
∴AD=5;
(3)
解:∵y=﹣ ![]() x2+
x2+ ![]() x,
x,
∴其對稱軸為x=5,
∵A、O兩點關于對稱軸對稱,
∴PA=PO,
當P、O、D三點在一條直線上時,PA+PD=PO+PD=OD,此時△PAD的周長最小,
如圖,連接OD交對稱軸于點P,則該點即為滿足條件的點P,
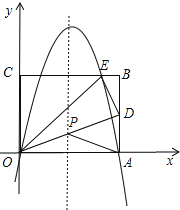
由(2)可知D點的坐標為(10,5),
設直線OD解析式為y=kx,把D點坐標代入可得5=10k,解得k= ![]() ,
,
∴直線OD解析式為y= ![]() x,
x,
令x=5,可得y= ![]() ,
,
∴P點坐標為(5, ![]() )
)
【解析】(1)利用矩形的性質和B點的坐標可求出A點的坐標,再利用待定系數法可求得拋物線的解析式;(2)設AD=x,利用折疊的性質可知DE=AD,在Rt△BDE中,利用勾股定理可得到關于x的方程,可求得AD的長;(3)由于O、A兩點關于對稱軸對稱,所以連接OD,與對稱軸的交點即為滿足條件的點P,利用待定系數法可求得直線OD的解析式,再由拋物線解析式可求得對稱軸方程,從而可求得P點坐標.本題主要考查二次函數的綜合應用,涉及知識點有待定系數法、矩形的性質、勾股定理、軸對稱的性質及方程思想.在(2)中注意方程思想的應用,在(3)中確定出滿足條件的P點的位置是解題的關鍵.本題考查知識點雖然較多,但題目屬于基礎性的題目,難度不大.
【考點精析】關于本題考查的勾股定理的概念和矩形的性質,需要了解直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2;矩形的四個角都是直角,矩形的對角線相等才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC=90°,點M是AC的中點,以AB為直徑作⊙O分別交AC,BM于點D,E.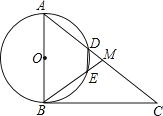
(1)求證:MD=ME;
(2)填空:
①若AB=6,當AD=2DM時,DE=;
②連接OD,OE,當∠A的度數為時,四邊形ODME是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知△ABC三個頂點的坐標分別是A(2,2),B(4,0),C(4,﹣4)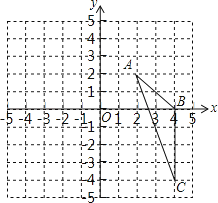
(1)請畫出△ABC向左平移6個單位長度后得到的△A1B1C1;
(2)以點O為位似中心,將△ABC縮小為原來的 ![]() ,得到△A2B2C2 , 請在y軸右側畫出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 請在y軸右側畫出△A2B2C2 , 并求出∠A2C2B2的正弦值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點B在線段AC上,點E在線段BD上,∠ABD=∠DBC=90°,AB=DB,EB=CB,M,N分別是AE,CD的中點.
(1)求證:△ABM≌△DBN;
(2)試探索BM和BN的關系,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,則三個結論:①AS=AR,②QP∥AR,③△BPR≌△QPS中一定正確的是( )

A. 全部正確 B. 僅①和②正確 C. 僅①正確 D. 僅①和③正確
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上,老師出示了如下的題目:如圖(1),在等邊△ABC中,點E在AB上,點D在CB的延長線上,且ED=EC,試判斷AE和BD的大小關系,并說明理由.
小敏與同桌小聰討論后,進行了如下解答:
(1)特殊情況,探索結論
當點E為AB的中點時,如圖(2),確定線段AE與DB的大小關系,請你直接寫出結論:AE DB(填“>”,“<”或“=”);
(2)特例啟發,解答題目
如圖(1),試判斷AE和BD的大小關系,并說明理由;
(3)拓展結論,設計新題
在等邊三角形ABC中,點E在直線AB上,點D在直線BC上,且ED=EC;若△ABC的邊長為1,AE=2,請畫出圖形,求CD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AC=3,BC=4,點O是BC中點,將△ABC繞點O旋轉得△A′B' C′,則在旋轉過程中點A、C′兩點間的最大距離是_______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCO是平行四邊形,OA=2,AB=6,點C在x軸的負半軸上,將ABCO繞點A逆時針旋轉得到ADEF,AD經過點O,點F恰好落在x軸的正半軸上,若點D在反比例函數y= ![]() (x<0)的圖象上,則k的值為
(x<0)的圖象上,則k的值為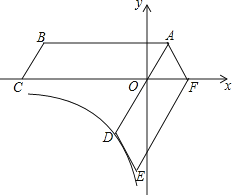
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com