
【題目】如圖,把矩形ABCD沿EF翻折,點B恰好落在AD邊的B′處,若AE=2,DE=6,∠EFB=60°,則矩形ABCD的面積是( ) 
A.12
B.24
C.12 ![]()
D.16 ![]()
【答案】D
【解析】解:在矩形ABCD中,
∵AD∥BC,
∴∠DEF=∠EFB=60°,
∵把矩形ABCD沿EF翻折點B恰好落在AD邊的B′處,
∴∠DEF=∠EFB=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,
AB=A′B′,
在△EFB′中,
∵∠DEF=∠EFB=∠EB′F=60°
∴△EFB′是等邊三角形,
Rt△A′EB′中,
∵∠A′B′E=90°﹣60°=30°,
∴B′E=2A′E,而A′E=2,
∴B′E=4,
∴A′B′=2 ![]() ,即AB=2
,即AB=2 ![]() ,
,
∵AE=2,DE=6,
∴AD=AE+DE=2+6=8,
∴矩形ABCD的面積=ABAD=2 ![]() ×8=16
×8=16 ![]() .
.
故選D.
解:在矩形ABCD中根據AD∥BC得出∠DEF=∠EFB=60°,由于把矩形ABCD沿EF翻折點B恰好落在AD邊的B′處,
所以∠EFB=∠DEF=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,
在△EFB′中可知∠DEF=∠EFB=∠EB′F=60°故△EFB′是等邊三角形,由此可得出∠A′B′E=90°﹣60°=30°,根據直角三角形的性質得出A′B′=AB=2 ![]() ,然后根據矩形的面積公式列式計算即可得解.
,然后根據矩形的面積公式列式計算即可得解.


科目:初中數學 來源: 題型:
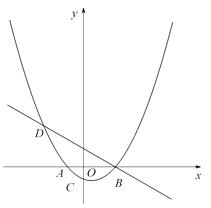
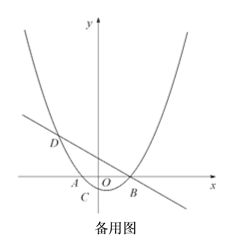
【題目】如圖,已知拋物線![]() (a為常數,且a>0)與x軸從左至右依次交于A,B兩點,與y軸交于點C,經過點B的直線
(a為常數,且a>0)與x軸從左至右依次交于A,B兩點,與y軸交于點C,經過點B的直線![]() 與拋物線的另一交點為D,且點D的橫坐標為﹣5.
與拋物線的另一交點為D,且點D的橫坐標為﹣5.
(1)求拋物線的函數表達式;
(2)P為直線BD下方的拋物線上的一點,連接PD、PB, 求△PBD面積的最大值.
(3)設F為線段BD上一點(不含端點),連接AF,一動點M從點A出發,沿線段AF以每秒1個單位的速度運動到F,再沿線段FD以每秒2個單位的速度運動到D后停止,當點F的坐標是多少時,點M在整個運動過程中用時最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】出租車司機小傅某天下午營運全是在東西走向的大道上行駛的,如果規定向東為正,行車里程(單位:km)如下:
+11, -2, +3, +9, -11, +5, -15, -8
(1)當把最后一名乘客送到目的地時,小傅距離出車地點的距離為多少?
(2)若每千米的營運額為5元,成本為2.7元/km,則這天下午他盈利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(11·柳州)在平面直角坐標系中,將點A (-2,1)向左平移2個單位到點Q,則點Q的坐標為
A.(-2,3)B.(0,1)C.(-4,1)D.(-4,-1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將函數y=﹣3x的圖象沿y軸向上平移2個單位長度后,所得圖象對應的函數關系式為( )
A.y=﹣3x+2
B.y=﹣3x﹣2
C.y=﹣3(x+2)
D.y=﹣3(x﹣2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知頂點為(﹣3,﹣6)的拋物線y=ax2+bx+c經過點(﹣1,﹣4),則下列結論中錯誤的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若點(﹣2,m),(﹣5,n)在拋物線上,則m>n
D. 關于x的一元二次方程ax2+bx+c=﹣4的兩根為﹣5和﹣1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com