
【題目】如圖①,直角三角形ABC中,∠B=90°.將它放在平面直角坐標系中,A(0,1),且滿足(AB-4)2+![]() =0.
=0.
(1)求直線AC的解析式.
(2)在直線BC上是否存在點P,使S△APC= 6?若存在,求P點坐標;若不存在,說明理由.
(3)如果M在y軸上,且△AMC是以AC為腰的等腰三角形,求M的坐標
(4)如果D是AC的中點,問在y軸上是否存在點M,使得MD+ ![]() AC最小?存在的話,請直接寫出M的坐標。
AC最小?存在的話,請直接寫出M的坐標。

 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:初中數學 來源: 題型:
【題目】選取二次三項式![]() 中的兩項,配成完全平方式的過程叫做配方.例如
中的兩項,配成完全平方式的過程叫做配方.例如
①選取二次項和一次項配方:![]() ;
;
②選取二次項和常數項配方:![]() ,或
,或![]() ;
;
③選取一次項和常數項配方:![]() .
.
根據上述材料,解決下面問題:
![]() 寫出
寫出![]() 的兩種不同形式的配方;
的兩種不同形式的配方;
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若關于
若關于![]() 的代數式
的代數式![]() 是完全平方式,求
是完全平方式,求![]() 的值;
的值;
![]() 用配方法證明:無論
用配方法證明:無論![]() 取什么實數時,總有
取什么實數時,總有![]() 恒成立.
恒成立.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O是等邊![]() 內一點
內一點![]() 將
將![]() 繞點C按順時針方向旋轉
繞點C按順時針方向旋轉![]() 得
得![]() ,連接
,連接![]() 已知
已知![]()
![]() .
.
![]() 求證:
求證:![]() 是等邊三角形;
是等邊三角形;
![]() 當
當![]() 時,試判斷
時,試判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
![]() 探究:當
探究:當![]() 為多少度時,
為多少度時,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,∠B=90°,AB=2,BC=1,CD=2,AD=3,連接AC.
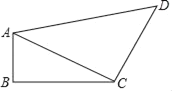
(1)求AC的長;
(2)判斷三角形ACD的形狀,并求出四邊形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】周末,小明騎自行車從家里出發到野外郊游.從家出發1小時后到達南亞所(景點),游玩一段時間后按原速前往湖光巖.小明離家1小時50分鐘,媽媽駕車沿相同路線前往湖光巖,如圖是他們離家的路程y(km)與小明離家時間x(h)的函數圖象.

(1)求小明騎車的速度和在南亞所游玩的時間;
(2)若媽媽在出發后25分鐘時,剛好在湖光巖門口追上小明,求媽媽駕車的速度及CD所在直線的函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市創建“綠色發展模范城市”,針對境內長江段兩種主要污染源:生活污水和沿江工廠污染物排放,分別用“生活污水集中處理”(下稱甲方案)和“沿江工廠轉型升級”(下稱乙方案)進行治理,若江水污染指數記為Q,沿江工廠用乙方案進行一次性治理(當年完工),從當年開始,所治理的每家工廠一年降低的Q值都以平均值n計算.第一年有40家工廠用乙方案治理,共使Q值降低了12.經過三年治理,境內長江水質明顯改善.
(1)求n的值;
(2)從第二年起,每年用乙方案新治理的工廠數量比上一年都增加相同的百分數m,三年來用乙方案治理的工廠數量共190家,求m的值,并計算第二年用乙方案新治理的工廠數量;
(3)該市生活污水用甲方案治理,從第二年起,每年因此降低的Q值比上一年都增加個相同的數值a.在(2)的情況下,第二年,用乙方案所治理的工廠合計降低的Q值與當年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有兩個可以自由轉動的均勻轉盤A、B,轉盤A被均勻地分成4等份,每份分別標上1、2、3、4四個數字;轉盤B被均勻地分成6等份,每份分別標上1、2、3、4、5、6六個數字。有人為甲、乙兩人設計了一個游戲,其規則如下:
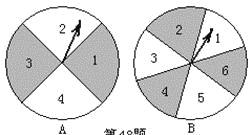
同時自由轉動轉盤A與B轉盤停止后,指針各指向一個數字(如果指針恰好指在分格線上,那么重轉一次,直到指針停留在某一數字為止),用所指的兩個數字作乘積,如果得到的積是偶數,那么甲勝;如果得到的積是奇數,那么乙勝(如轉盤A指針指向3,轉盤B指針指向5,3×5=15,按規則乙勝)。你認為這樣的規則是否公平?請說明理由;如果不公平,請你設計一個公平的規則,并說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于![]() 的一元二次方程
的一元二次方程![]() .
.
![]() 若方程有實數根,求
若方程有實數根,求![]() 的取值范圍;
的取值范圍;
![]() 如果
如果![]() 是滿足條件的最大的整數,且方程
是滿足條件的最大的整數,且方程![]() 一根的相反數是一元二次方程
一根的相反數是一元二次方程![]() 的一個根,求
的一個根,求![]() 的值及這個方程的另一根.
的值及這個方程的另一根.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com