
 =
= 時,求
時,求 的值;
的值; 時,①
時,① =______;②證明:∠BPC=∠A;
=______;②證明:∠BPC=∠A; 時,直接寫出tan∠BPC的值.
時,直接寫出tan∠BPC的值.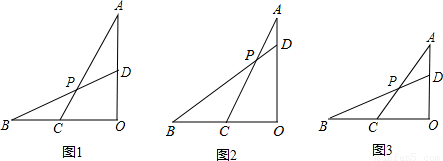
 =
= ,又
,又 =
= 得AD=DO,則有AD=2DE,即可得到
得AD=DO,則有AD=2DE,即可得到 =2;
=2; =
= 則DO=3AD,得2DE=3AD即AD=
則DO=3AD,得2DE=3AD即AD= DE,則
DE,則 =
= ;②設OB=8a,則OA=OB=8a,OC=4a,AD=2a,DE=OE=3a,根據勾股定理得到CE=
;②設OB=8a,則OA=OB=8a,OC=4a,AD=2a,DE=OE=3a,根據勾股定理得到CE= =5a,則有EC=EA,得到∠ACE=∠A,而∠BPC=∠ACE,即可得到結論;
=5a,則有EC=EA,得到∠ACE=∠A,而∠BPC=∠ACE,即可得到結論; ,由點C為OB中點,則CO=a
,由點C為OB中點,則CO=a ,利用勾股定理可計算得AC=
,利用勾股定理可計算得AC= a,易證得Rt△ADF∽Rt△ACO,得到AF:AO=DF:OC=AD:AC,即AF:na=DF:
a,易證得Rt△ADF∽Rt△ACO,得到AF:AO=DF:OC=AD:AC,即AF:na=DF: a=a:
a=a: a,求出AF=
a,求出AF= a,DF=
a,DF= ,再根據平行線分線段成比例定理得到AP:AC=AD:AE,即AP:
,再根據平行線分線段成比例定理得到AP:AC=AD:AE,即AP: a=a:
a=a: a,求出AP=
a,求出AP= ,則PF=AP-AF=
,則PF=AP-AF=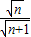 a,然后根據正切的定義即可得到tan∠FPD,從而得到tan∠BPC的值.
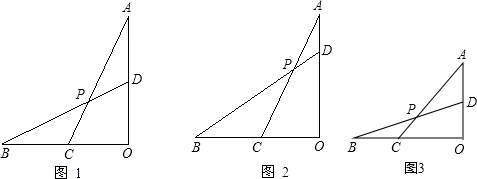
a,然后根據正切的定義即可得到tan∠FPD,從而得到tan∠BPC的值. 解:(1)過C作CE∥BD交AO于點E,如圖,
解:(1)過C作CE∥BD交AO于點E,如圖,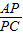 =
= ,
, =
= ,
, =2;
=2; =
= ,
, =
= ,
, DE,
DE, =
= ;
; =5a,
=5a, ;
; ,
, ,
, =
= a,
a, a=a:
a=a: a,
a, a,DF=
a,DF= ,
, a=a:
a=a: a,
a, ,
, a,
a, =
=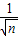 =
= .
. .
.

科目:初中數學 來源: 題型:
| AP |
| PC |
| AD |
| AO |
| 1 |
| 4 |
| n |
查看答案和解析>>
科目:初中數學 來源: 題型:
| AD |
| AO |
| 1 |
| 2 |
| AP |
| PC |
| AD |
| AO |
| 1 |
| 4 |
| AP |
| PC |
| 2 |
| 3 |
| 2 |
| 3 |
| n |

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
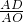 =
= 時,求
時,求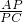 的值;
的值;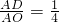 時,①
時,①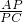 =______;②證明:∠BPC=∠A;
=______;②證明:∠BPC=∠A;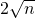 時,直接寫出tan∠BPC的值.
時,直接寫出tan∠BPC的值.
查看答案和解析>>
科目:初中數學 來源:第24章《相似形》中考題集(03):24.1 比例線段(解析版) 題型:解答題
 的值;
的值; 時,求tan∠BPC的值.
時,求tan∠BPC的值. 時,直接寫出tan∠BPC的值.
時,直接寫出tan∠BPC的值.
查看答案和解析>>
科目:初中數學 來源:2013年5月中考數學模擬試卷(4)(解析版) 題型:解答題
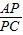 的值;
的值; 時,求tan∠BPC的值.
時,求tan∠BPC的值. 時,直接寫出tan∠BPC的值.
時,直接寫出tan∠BPC的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com