
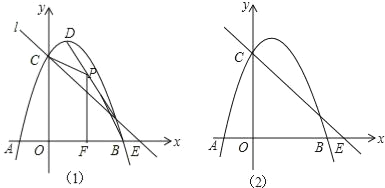
【題目】如圖1,拋物線y=﹣x2+2x+3與x軸交于A,B,與y軸交于C,拋物線的頂點為D,直線l過C交x軸于E(4,0).
(1)寫出D的坐標和直線l的解析式;
(2)P(x,y)是線段BD上的動點(不與B,D重合),PF⊥x軸于F,設四邊形OFPC的面積為S,求S與x之間的函數關系式,并求S的最大值;
(3)點Q在x軸的正半軸上運動,過Q作y軸的平行線,交直線l于M,交拋物線于N,連接CN,將△CMN沿CN翻轉,M的對應點為M′.在圖2中探究:是否存在點Q,使得M′恰好落在y軸上?若存在,請求出Q的坐標;若不存在,請說明理由.
【答案】(1)y=﹣![]() x+3;(2)
x+3;(2)![]() ;(3)點Q的坐標為(
;(3)點Q的坐標為(![]() ,0)或(4,0).
,0)或(4,0).
【解析】試題(1)先把拋物線解析式配成頂點式即可得到D點坐標,再求出C點坐標,然后利用待定系數法求直線l的解析式;
(2)先根據拋物線與x軸的交點問題求出B(3,0),再利用待定系數法求出直線BD的解析式為y=-2x+6,則P(x,-2x+6),然后根據梯形的面積公式可得S=-x2+![]() x(1≤x≤3),再利用而此函數的性質求S的最大值;
x(1≤x≤3),再利用而此函數的性質求S的最大值;
(3)如圖2,設Q(t,0)(t>0),則可表示出M(t,-![]() t+3),N(t,-t2+2t+3),利用兩點間的距離公式得到MN=|t2-
t+3),N(t,-t2+2t+3),利用兩點間的距離公式得到MN=|t2-![]() t|,CM=
t|,CM=![]() t,然后證明NM=CM得到|t2-
t,然后證明NM=CM得到|t2-![]() t|=
t|=![]() t,再解絕對值方程求滿足條件的t的值,從而得到點Q的坐標.
t,再解絕對值方程求滿足條件的t的值,從而得到點Q的坐標.
試題解析:(1)∵y=-x2+2x+3=-(x-1)2+4,
∴D(1,4),
當x=0時,y=-x2+2x+3=3,則C(0,3),
設直線l的解析式為y=kx+b,
把C(0,3),E(4,0)分別代入得![]() ,解得
,解得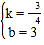 ,
,
∴直線l的解析式為y=-![]() x+3;
x+3;
(2)如圖(1),當y=0時,-x2+2x+3=0,解得x1=-1,x2=3,則B(3,0),
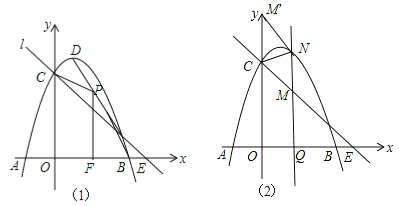
設直線BD的解析式為y=mx+n,
把B(3,0),D(1,4)分別代入得![]() ,解得
,解得![]() ,
,
∴直線BD的解析式為y=-2x+6,
則P(x,-2x+6),
∴S=![]()
![]() (-2x+6+3)
(-2x+6+3)![]() x=-x2+
x=-x2+![]() x(1≤x≤3),
x(1≤x≤3),
∵S=-(x-![]() )2+
)2+![]() ,
,
∴當x=![]() 時,S有最大值,最大值為
時,S有最大值,最大值為![]() ;
;
(3)存在.
如圖2,設Q(t,0)(t>0),則M(t,-![]() t+3),N(t,-t2+2t+3),
t+3),N(t,-t2+2t+3),
∴MN=|-t2+2t+3-(-![]() t+3)|=|t2-
t+3)|=|t2-![]() t|,
t|,
CM=![]() =
=![]() t,
t,
∵△CMN沿CN翻轉,M的對應點為M′,M′落在y軸上,
而QN∥y軸,
∴MN∥CM′,NM=NM′,CM′=CM,∠CNM=∠CNM′,
∴∠M′CN=∠CNM,
∴∠M′CN=∠CNM′,
∴CM′=NM′,
∴NM=CM,
∴|t2-![]() t|=
t|=![]() t,
t,
當t2-![]() t=
t=![]() t,解得t1=0(舍去),t2=4,此時Q點坐標為(4,0);
t,解得t1=0(舍去),t2=4,此時Q點坐標為(4,0);
當t2-![]() t=-
t=-![]() t,解得t1=0(舍去),t2=
t,解得t1=0(舍去),t2=![]() ,此時Q點坐標為(
,此時Q點坐標為(![]() ,0),
,0),
綜上所述,點Q的坐標為(![]() ,0)或(4,0).
,0)或(4,0).


科目:初中數學 來源: 題型:
【題目】為推動全面健身,縣政府在城南新城新建體育休閑公園,公園設有A、B、C、D四個出入口供廣大市民進出.
(1)小明的爸爸去公園進行體育鍛煉,從出入口A進入的概率是________;
(2)張老師和小明的爸爸一起約定去參加鍛煉,請用畫樹狀圖或列表法求他們選擇從不同出入口進體育場的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,![]() 是直角,
是直角,![]() 在
在![]() 的外側,且
的外側,且![]() ,
,![]() 是
是![]() 的平分線,
的平分線,![]() 是
是![]() 的平分線.
的平分線.
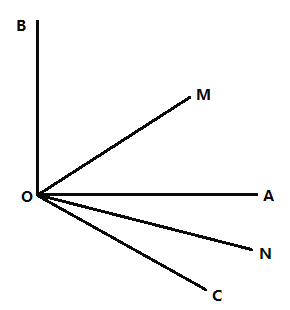
(1)求![]() 的大小;
的大小;
(2)當銳角![]() 的大小為
的大小為![]() 時,試猜想(1)中
時,試猜想(1)中![]() 的大小是否發生改變?并通過計算說明理由.
的大小是否發生改變?并通過計算說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
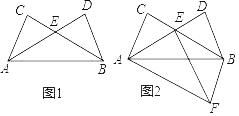
【題目】如圖1,點C、D是線段AB同側兩點,且AC=BD,∠CAB=∠DBA,連接BC,AD交于點 E.
(1)求證:AE=BE;
(2)如圖2,△ABF與△ABD關于直線AB對稱,連接EF.
①判斷四邊形ACBF的形狀,并說明理由;
②若∠DAB=30°,AE=5,DE=3,求線段EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
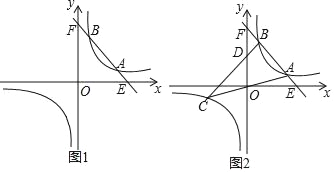
【題目】已知:一次函數y=﹣2x+10的圖象與反比例函數y=![]() (k>0)的圖象相交于A、B兩點(A的B的右側).
(k>0)的圖象相交于A、B兩點(A的B的右側).
(1)當A(4,2)時,求反比例函數的解析式:
(2)當A的橫坐標是3,B的橫坐標是2時,直線OA與此反比例函數圖象的另一支交于另一點C,連接BC交y軸于點D.
①求C點的坐標;
②求D點的坐標;
③求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
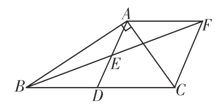
【題目】如圖,在Rt△ABC中,∠BAC=90°,D是BC的中點,E是AD的中點,過點A作AF∥BC交BE的延長線于點F.
(1)求證:△AEF≌△DEB;
(2)求證:四邊形ADCF是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司購買了一批A、B兩種型號的產品,其中A型產品的單價比B型產品的單價多6元,已知該公司用1400元購買A型產品的件數與用1160元購買B型產品的件數相等.
(1)求該公司購買的A、B兩種型號產品的單價各是多少元?
(2)若兩種型號的產品共購買了100件,且購買的總費用為3260元,求購買了多少件A型產品?
查看答案和解析>>
科目:初中數學 來源: 題型:
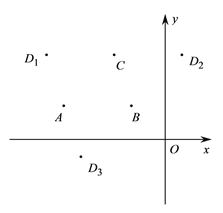
【題目】在平面直角坐標系![]() 中,已知點
中,已知點![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,以點
,以點![]() 為頂點的平行四邊形有三個,記第四個頂點分別為
為頂點的平行四邊形有三個,記第四個頂點分別為![]() ,如圖所示.
,如圖所示.
(1)若![]() ,則點
,則點![]() 的坐標分別是( ),( ),( );
的坐標分別是( ),( ),( );
(2)是否存在點![]() ,使得點
,使得點![]() 在同一條拋物線上?若存在,求出點
在同一條拋物線上?若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校學生會為積極響應武漢市文明創建活動,組織有關方面的知識競賽,共設有20道選擇題,各題分值相同,每題必答,下表記錄了3個參賽者的得分情況.
參賽者 | 答對題數 | 答錯題數 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 18 | 2 | 88 |
(1)設答對一題記a分,答錯一題記b分,則a= b= ;
(2)參賽者E說他得了80分,你認為可能嗎,為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com