
 經過A、C兩點.
經過A、C兩點.
 解:(1)連接CH,
解:(1)連接CH, x+3過A、C,則OC=3,AO=4,
x+3過A、C,則OC=3,AO=4, ;
;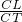 =
= ,
, )×3=
)×3=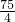 .
.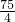 .
. x+3過A、C,從而得出tan∠CNM的值.
x+3過A、C,從而得出tan∠CNM的值.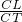 =
= ,從而得出CS•CT的值不變,是定值.
,從而得出CS•CT的值不變,是定值.

 寒假學與練系列答案
寒假學與練系列答案科目:初中數學 來源: 題型:
| k |
| x |
| k |
| x |
| 10 |
| 7 |

查看答案和解析>>
科目:初中數學 來源:2011-2012學年甘肅省蘭州四中九年級(上)期中數學試卷(解析版) 題型:解答題
 的圖象的一個分支位于第一象限.
的圖象的一個分支位于第一象限.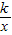 的圖象的圖象上,求k的值;
的圖象的圖象上,求k的值; S1?
S1?
查看答案和解析>>
科目:初中數學 來源:2012年初中畢業升學考試(四川巴中卷)數學(解析版) 題型:解答題
如圖,在平面直角坐標系中,一次函數 的圖象與y軸交于點A,
的圖象與y軸交于點A,
與x軸交于點B,與反比例函數 的圖象分別交于點M,N,已知△AOB的面積為1,點M的縱坐
的圖象分別交于點M,N,已知△AOB的面積為1,點M的縱坐
標為2,
(1)求一次函數和反比例函數的解析式;
(2)直接寫出 時x的取值范圍。
時x的取值范圍。

查看答案和解析>>
科目:初中數學 來源:2013屆安徽滁州八年級下期末模擬數學試卷(滬科版)(解析版) 題型:解答題
已知:如圖1,平面直角坐標系 中,四邊形OABC是矩形,點A,C的坐
中,四邊形OABC是矩形,點A,C的坐
標分別為(6,0),(0,2).點D是線段BC上的一個動點(點D與點B,C不重合),過點D作直線 =-
=- +
+ 交折線O-A-B于點E.
交折線O-A-B于點E.
(1)在點D運動的過程中,若△ODE的面積為S,求S與 的函數關系式,并寫出自變量的取值范圍;
的函數關系式,并寫出自變量的取值范圍;
(2)如圖2,當點E在線段OA上時,矩形OABC關于直線DE對稱的圖形為矩形O′A′B′C′,C′B′分別交CB,OA于點D,M,O′A′分別交CB,OA于點N,E.求證:四邊形DMEN是菱形;
(3)問題(2)中的四邊形DMEN中,ME的長為____________.


查看答案和解析>>
科目:初中數學 來源:2011年初中畢業升學考試(廣西欽州卷)數學 題型:解答題
(本題滿分8分)已知四邊形ABCD是邊長為4的正方形,以AB為直徑在正方形內作半圓,P是半圓上的動點(不與點A、B重合),連接PA、PB、PC、PD.
(1)如圖①,當PA的長度等于
時,∠PAB=60°;
當PA的長度等于 時,△PAD是等腰三角形;
(2)如圖②,以AB邊所在直線為x軸、AD邊所在直線為y軸,建立如圖所示的直角
坐標系(點A即為原點O),把△PAD、△PAB、△PBC的面積分別記為S1、S2、S3.坐
標為(a,b),試求2 S1 S3-S22的最大值,并求出此時a,b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com