
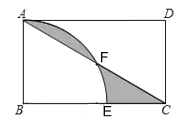
【題目】如圖,在矩形![]() 中,連接
中,連接![]() ,以點
,以點![]() 為圓心,
為圓心,![]() 為半徑畫弧,交
為半徑畫弧,交![]() 于點
于點![]() ,已知
,已知![]() ,
,![]() ,則圖中陰影部分的面積為_______.(結果保留
,則圖中陰影部分的面積為_______.(結果保留![]() )
)
【答案】![]()
【解析】
設圓弧與AC交于F,連接BF,過F作FH⊥BC于H,解直角三角形得到∠BAC=60°,求得△ABF是等邊三角形,得到∠ABF=60°,推出∠FBE=30°,然后根據S陰影=S扇形BAF+S△BCFS△ABFS扇形BFE=S扇形BAF S扇形BFE計算即可.2
解:設圓弧與AC交于F,連接BF,過F作FH⊥BC于H,
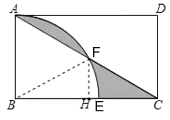
在矩形ABCD中,∵∠ABC=90°,AB=BE=3,BC=![]() ,
,
∴tan∠BAC=![]() ,
,
∴∠BAC=60°,
∵BA=BF=3,
∴△ABF是等邊三角形,
∴∠ABF=60°,
∴∠FBH=30°,
∴FH=![]() BF=
BF=![]() ,
,
∴S陰影=S扇形BAF+S△BCFS△ABFS扇形BFE=S扇形BAF S扇形BFE ![]() ,
,
故答案為:![]() .
.


 寒假學與練系列答案
寒假學與練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在每個小正方形的邊長為1的網格中,![]() 的頂點A在格點上,B是小正方形邊的中點,
的頂點A在格點上,B是小正方形邊的中點,![]() ,
,![]() ,經過點A,B的圓的圓心在邊AC上.
,經過點A,B的圓的圓心在邊AC上.
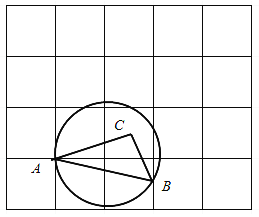
(Ⅰ)線段AB的長等于_______________;
(Ⅱ)請用無刻度的直尺,在如圖所示的網格中,畫出一個點P,使其滿足![]() ,并簡要說明點P的位置是如何找到的(不要求證明)_____.
,并簡要說明點P的位置是如何找到的(不要求證明)_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
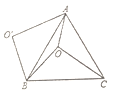
【題目】如圖,O是等邊![]() 內一點,
內一點,![]() ,以點B為旋轉中心,將線段BO逆時針旋轉
,以點B為旋轉中心,將線段BO逆時針旋轉![]() 得到線段
得到線段![]() ,連接
,連接![]() ,則下列結論:
,則下列結論:
①![]() 可以由
可以由![]() 繞點B逆時針旋轉
繞點B逆時針旋轉![]() 得到
得到
②連接![]() ,則
,則![]()
③![]()
④![]()
其中正確的結論是____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知C是線段AB上的一點,分別以AC、BC為邊在線段AB同側作正方形ACDE和正方形CBGF,點F在CD上,聯結AF、BD,BD與FG交于點M,點N是邊AC上的一點,聯結EN交AF 與點H.
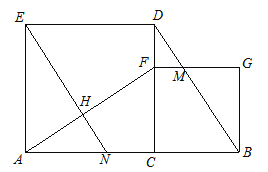
(1)求證:AF=BD;
(2)如果![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】暑假旅游旺季即將到來,外出旅游的人數不斷攀升,去海邊游玩是大多數人不錯的選擇,去海邊游玩的人都會選擇自己購買海產品進行加工,某商家7月1日進購了一批扇貝與爬爬蝦共計200千克,已知扇貝進價10元/千克,售價30元/千克,爬爬蝦進價20元/千克,售價30元/千克.
(1)若這批海產品全部售完獲利不低于3000元,則扇貝至少進購多少千克?
(2)第一批扇貝和爬爬蝦很快售完,于是商家決定購進第二批扇貝與爬爬蝦,兩種海產品的進價不變,扇貝售價比第一批上漲![]() ,爬爬蝦售價比第一批上漲
,爬爬蝦售價比第一批上漲![]() ,銷量與(1)中獲得最低利潤時的銷量相比,扇貝的銷量下降了
,銷量與(1)中獲得最低利潤時的銷量相比,扇貝的銷量下降了![]() ,爬爬蝦的銷量不變,結果第二批已經賣掉的扇貝與爬爬蝦的銷售總額比(1)中第一批扇貝與爬爬蝦售完后對應的最低銷售總額增加了
,爬爬蝦的銷量不變,結果第二批已經賣掉的扇貝與爬爬蝦的銷售總額比(1)中第一批扇貝與爬爬蝦售完后對應的最低銷售總額增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為迎接2022年冬奧會,鼓勵更多的大學生參與到志愿服務中,甲、乙兩所學校組織了志愿服務團隊選拔活動,經過初選,兩所學校各有300名學生進入綜合素質展示環節,為了了解這些學生的整體情況,從兩校進入綜合素質展示環節的學生中分別隨機抽取了50名學生的綜合素質展示成績(百分制),并對數據(成績)進行整理、描述和分析,下面給出了部分信息.
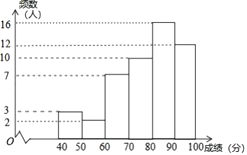
a.甲學校學生成績的頻數分布直方圖如圖(數據分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲學校學生成績在![]() 這一組是:
這一組是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙學校學生成績的平均數、中位數、眾數、優秀率(85分及以上為優秀)如下:
平均數 | 中位數 | 眾數 | 優秀率 |
83.3 | 84 | 78 | 46% |
根據以上信息,回答下列問題:
(1)甲學校學生![]() ,乙學校學生
,乙學校學生![]() 的綜合素質展示成績同為82分,這兩人在本校學生中綜合素質展示排名更靠前的是________(填“
的綜合素質展示成績同為82分,這兩人在本校學生中綜合素質展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根據上述信息,推斷________學校綜合素質展示的水平更高,理由為:__________________________
(至少從兩個不同的角度說明推斷的合理性).
(3)若每所學校綜合素質展示的前120名學生將被選入志愿服務團隊,預估甲學校分數至少達到________分的學生才可以入選.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】發現思考:已知等腰三角形ABC的兩邊分別是方程x2﹣7x+10=0的兩個根,求等腰三角形ABC三條邊的長各是多少?下邊是涵涵同學的作業,老師說他的做法有錯誤,請你找出錯誤之處并說明錯誤原因.
涵涵的作業
解:x2﹣7x+10=0
a=1 b=﹣7 c=10
∵b2﹣4ac=9>0
∴x=![]() =
=![]()
∴x1=5,x2=2
所以,當腰為5,底為2時,等腰三角形的三條邊為5,5,2.
當腰為2,底為5時,等腰三角形的三條邊為2,2,5.
探究應用:請解答以下問題:
已知等腰三角形ABC的兩邊是關于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的兩個實數根.
=0的兩個實數根.
(1)當m=2時,求△ABC的周長;
(2)當△ABC為等邊三角形時,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABE和△ACF中,EB交AC于點M,交FC于點D,AB交FC于點N,∠E=∠F=90°,∠B=∠C,AE=AF.下列結論:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正確的是_________.(填序號)
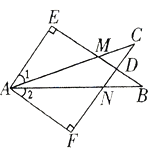
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com