
【題目】在等腰直角三角形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是斜邊
是斜邊![]() 的中點,連接
的中點,連接![]() .
.
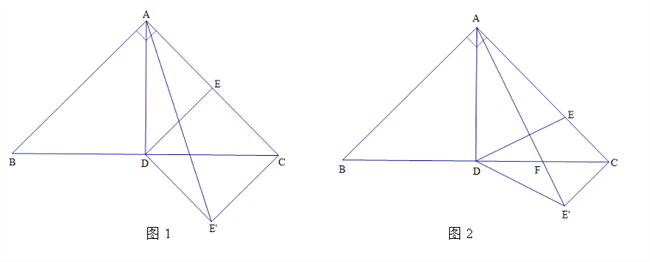
(1)如圖1, ![]() 是
是![]() 的中點,連接
的中點,連接![]() ,將
,將![]() 沿
沿![]() 翻折到
翻折到![]() ,連接
,連接![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
(2)如圖2,在![]() 上取一點
上取一點![]() ,使得
,使得![]() ,連接
,連接![]() ,將
,將![]() 沿
沿![]() 翻折到
翻折到![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,求證:
,求證: ![]() .
.
【答案】(1)![]() 的值為
的值為![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】試題分析:(1)在等腰直角三角形中先求出AC的長,再在Rt△ACE′中,理由勾股定理求出AE′的長即可;(2)B作AE’的垂線交AD于點G,交AC于點H,由角角邊可證△ABH≌△CAE′,所以AH=HE=CE,進而D是BC中點,由中位線定理得DE//BH ,再由角角邊得△ABG≌△CAF,得到AG=CF進而DF=CF.
試題解析:(1)∵![]() ,
, ![]() ,D是斜邊
,D是斜邊![]() 的中點,
的中點,
∴![]() ,∠ACD=45°,
,∠ACD=45°,
在RtADC中:AC=AD.sin45°=![]()
∵E是AC的中點
∴CE=![]() AC=
AC=![]()
∵將△CDE沿CD翻折到△CDE′
∴CE′=CE=![]() , ∠ACE′=90°,由勾股定理得:
, ∠ACE′=90°,由勾股定理得:
AE′=![]()
過B作AE’的垂線交AD于點G,交AC于點H
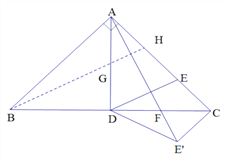
∵∠ABH+∠BAF=90°,∠CAF+∠BAF=90°
∴∠ABH=∠CAF
又∵AB=AC,∠BAH=∠ACE’=90°
∴△ABH≌△CAE′
∴AH=CE′=CE
∵![]()
∴AH=HE=CE
∵D是BC中點
∴DE//BH
∴G是AD中點
在ABG和CAF中:AB=AC,∠BAD=∠ACD=45°,∠ABH=∠CAF
∴△ABG≌△CAF
∴AG=CF
∵AG=![]() AD
AD
∴CF=![]() AD=
AD=![]() CD
CD
∴DF=CF


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,已知AD∥BC,AB⊥BC,點E,F在邊AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ![]() ,FC=2
,FC=2 ![]() .
. 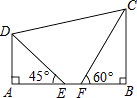
(1)BC= .
(2)求點D到BC的距離.
(3)求DC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應“書香校園”號召,重慶一中在九年級學生中隨機抽取某班學生對2016年全年閱讀中外名著的情況進行調查,整理調查結果發現,每名學生閱讀中外名著的本數,最少的有5本,最多的有8本,并根據調查結果繪制了如圖所示的不完整的折線統計圖和扇形統計圖.

(1)該班學生共有 名,扇形統計圖中閱讀中外名著本數為7本所對應的扇形圓心角的度數是 度,并補全折線統計圖;
(2)根據調查情況,班主任決定在閱讀中外名著本數為5本和8本的學生中任選兩名學生進行交流,請用樹狀圖或表格求出這兩名學生閱讀的本數均為8本的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數![]() 都可以進行這樣的分解:
都可以進行這樣的分解: ![]() (
(![]() ,
, ![]() 是正整數,且
是正整數,且![]() ),在
),在![]() 的所有這種分解中,如果
的所有這種分解中,如果![]() ,
, ![]() 兩因數之差的絕對值最小,我們就稱
兩因數之差的絕對值最小,我們就稱![]() 是
是![]() 的最佳分解,并規定:
的最佳分解,并規定: ![]() .
.
例如![]() 可以分解成
可以分解成![]() ,
, ![]() 或
或![]() ,因為
,因為![]() ,所以
,所以![]() 是
是![]() 的最佳分解,所以
的最佳分解,所以![]() .
.
(![]() )求出
)求出![]() 的值.
的值.
(![]() )如果一個兩位正整數
)如果一個兩位正整數![]() ,
, ![]() (
(![]() ,
, ![]() ,
, ![]() 為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為
為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為![]() ,那么我們稱這個數
,那么我們稱這個數![]() 為“文瀾數”,求所有“文瀾數”并寫出所有“文瀾數”中
為“文瀾數”,求所有“文瀾數”并寫出所有“文瀾數”中![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用描點法畫二次函數y=ax2+bx+c(a≠0)的圖象時,列出了如下表格:
x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
y=ax2+bx+c(a≠0) | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
那么當該二次函數值y > 0時,x的取值范圍是_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】[實際情境]李明家、王亮家、西山森林公園都位于石家莊市槐安路的沿線上,李明、王亮同學時分別從自己家出發,沿筆直的槐安路勻速騎行到達西山森林公園,李明的騎行速度是王亮的騎行速度的1.5倍.
[數學研究]設t(分鐘)后李明、王亮兩人與王亮家的距離分別為y1 . y2 , 則y1 . y2與t的函數關系圖象如圖所示,試根據圖象解決下列問題: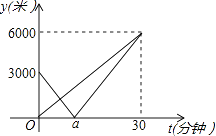
(1)填空:王亮的速度v2=米/分鐘;
(2)寫出y1與t的函數關系式;
(3)因為李明攜帶的無線對講機電量不足,只有在小于1000米范圍內才能和王亮的無線對講機清晰地通話,試探求什么時間段內兩人的無線對講機無法清晰通話.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com