【答案】
分析:(Ⅰ)設時間為t,則AP=BQ=t,PB=4-t;需要分類討論:①當∠PQB=90°時和②當∠BPQ=90°時兩種情況,然后在直角三角形中利用30°所對的直角邊是斜邊的一半可以求得t的值;
(Ⅱ)此題也需要分類討論:①當點P,Q分別在線段AB,BC上運動時,利用等邊三角形的性質和全等三角形(△ABQ≌△CAP)的判定與性質可以證得∠CMQ=60°不變;
②當點P,Q分別在射線AB,BC上運動時,利用等邊三角形的性質、全等三角形(△PBC≌△ACQ)的判定與性質可以證得∠CMQ=120°不變.
解答:解:(Ⅰ)設時間為t,則AP=BQ=t,PB=4-t
①當∠PQB=90°時,∵∠B=60°,∴PB=2BQ,得4-t=2t,解得,t=

;
②當∠BPQ=90°,∵∠B=60°,∴BQ=2PB,得t=2(4-t),解得t=

;
∴當AP=

cm或AP=

cm時,△PBQ為直角三角形--------------------------(4分)
(Ⅱ)①當點P,Q分別在線段AB,BC上運動時,∠CMQ=60°不變.
∵等邊△ABC中,AB=AC,∠B=∠CAP=60°,
又由條件得AP=BQ,∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP(全等三角形的對應角相等),
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°--------(6分)
②當點P,Q分別在射線AB,BC上運動時,∠CMQ=120°不變.
∵在等邊△ABC中,AB=AC,∠B=∠CAP=60°,
∴∠PBC=∠ACQ=120°,又由條件得BP=CQ,
∴△PBC≌△ACQ(SAS),
∴∠BPC=∠MQC(全等三角形的對應角相等),
又∵∠PCB=∠MCQ,
∴∠CMQ=∠PBC=120°(等量代換)-------------------------------------------------------------(10分)
點評:本題考查了等邊三角形的性質、全等三角形的判定與性質.解題時,采用了“分類討論”是數學思想,以防漏解.

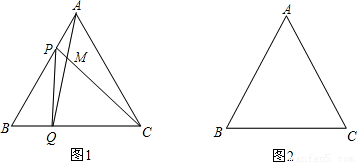
 ;
; ;
; cm或AP=
cm或AP= cm時,△PBQ為直角三角形--------------------------(4分)
cm時,△PBQ為直角三角形--------------------------(4分)




