
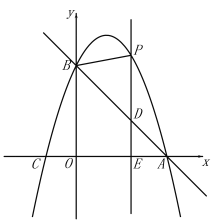
【題目】如圖,直線![]() 與x軸交于點A(3,0),與y軸交于點B,拋物線
與x軸交于點A(3,0),與y軸交于點B,拋物線![]() 經過A,B.
經過A,B.
(1)求拋物線解析式;
(2)E(m,0)是x軸上一動點,過點E作![]() 軸于點E,交直線AB于點D,交拋物線于點P,連接PB.
軸于點E,交直線AB于點D,交拋物線于點P,連接PB.
①點E在線段OA上運動,若△PBD是等腰三角形時,求點E的坐標;
②點E在x軸的正半軸上運動,若![]() ,請直接寫出m的值.
,請直接寫出m的值.
【答案】(1)![]() ;(2)①點E的坐標為
;(2)①點E的坐標為![]() ,
,![]() 或
或![]() ;②m的值為
;②m的值為![]() 或5
或5
【解析】
(1)把![]() 代入
代入![]() ,求出點B的坐標,再把
,求出點B的坐標,再把![]() 代入
代入![]() ,求出b,c的值即可;
,求出b,c的值即可;
(2)先求出![]() ,①分
,①分![]() ,
,![]() ,
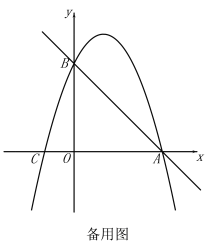
,![]() 三種情況分析即可;②先求出直線BC的解析式,當點P在x軸上方時,
三種情況分析即可;②先求出直線BC的解析式,當點P在x軸上方時,![]() ,可得出直線BP的解析式為:
,可得出直線BP的解析式為:![]() ,求出與拋物線的交點即可;當點P在x軸下方時,可得出直線BP的解析式為:
,求出與拋物線的交點即可;當點P在x軸下方時,可得出直線BP的解析式為:![]() ,求出與拋物線的交點即可.
,求出與拋物線的交點即可.
解:(1)把![]() 代入
代入![]() 得:
得:![]()
則B的坐標為![]() ,
,
把![]() 代入
代入![]() 中
中
得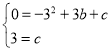
解得:![]()
∴拋物線的解析式的為:![]() .
.
(2) ∵![]()
∴![]()
又![]() 軸
軸
∴![]()
∴![]()
① 當![]() 時,如圖1,
時,如圖1,
∵△PBD是等腰直角三角形,
∴![]()
解得:![]() ;
;
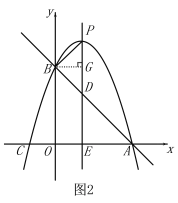
當![]() 時,如圖2,
時,如圖2,
過點B作BG⊥PD,△PBD是等腰直角三角形,
∴![]() .
.
∴![]() ,
,
解得:![]() ;
;
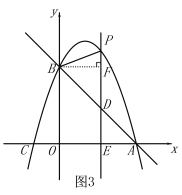
當![]() 時,如圖3,
時,如圖3,
過點B作BF⊥PD,△BFD是等腰直角三角形,
∴![]() .
.
∴![]() ,
,
解得:![]() ;
;

綜上所述,點E的坐標為![]() ,
,![]() 或
或![]() .
.
② 根據拋物線解析式可得出點![]()
∴直線CB的解析式為:![]()
當點P在x軸上方時,如圖1,
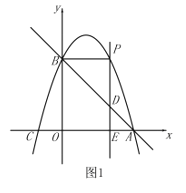
∵![]() ,
,![]()
∴![]()
∴直線BP的解析式為:![]()
∴![]()
解得:![]() (舍去)
(舍去)
當點P在x軸下方時,如下圖所示:
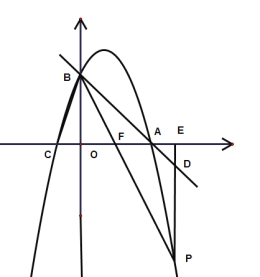
∵![]() ,
,![]()
∴![]()
∴![]()
∴直線BP的解析式為:![]()
∴![]()
解得:![]() (舍去)
(舍去)
∴m的值為![]() 或5.
或5.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:初中數學 來源: 題型:
【題目】對于某一函數給出如下定義:對于任意實數m, 當自變量x≥m時,函數y關于x的函數圖象為![]() ,將G沿直線x=m翻折后得到的函數圖象為
,將G沿直線x=m翻折后得到的函數圖象為![]() ,函數G的圖象由
,函數G的圖象由![]() 和
和![]() 兩部分共同組成,則函數G為原函數的“對折函數”,如函數y=x(x≥2)的對折函數為
兩部分共同組成,則函數G為原函數的“對折函數”,如函數y=x(x≥2)的對折函數為![]()
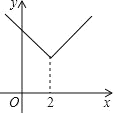
(1)寫出函數y =2x+1(x≥ 1)的對折函數;
(2)若函數y =2x2(x≥![]() )的對折函數與x軸交于點A,B(點A在點B的左側),與y軸交于點C,求△ABC的周長;
)的對折函數與x軸交于點A,B(點A在點B的左側),與y軸交于點C,求△ABC的周長;
(3)若點P(m,5)在函數y =![]() 4( x≥1)的對折函數的圖象上,求m的值;
4( x≥1)的對折函數的圖象上,求m的值;
(4)當函數y=![]() 4(x≥n)的對折函數與x軸有不同的交點個數時,直接寫出n的取值范圍
4(x≥n)的對折函數與x軸有不同的交點個數時,直接寫出n的取值范圍
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 是指一個國家(或地區)在一定時期內生產活動的最終成果,常被公認為是衡量經濟狀況的最佳指標.截止2020年4月27日,對除西藏外的30個省區市第一季度有關
是指一個國家(或地區)在一定時期內生產活動的最終成果,常被公認為是衡量經濟狀況的最佳指標.截止2020年4月27日,對除西藏外的30個省區市第一季度有關![]() 的數據進行收集、整理、描述和分析.下面給出了部分信息:
的數據進行收集、整理、描述和分析.下面給出了部分信息:
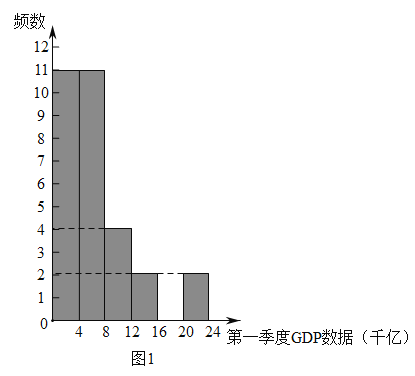
a.各省區市![]() 數據的頻數分布直方圖,如圖1(數據分成6組,各組是
數據的頻數分布直方圖,如圖1(數據分成6組,各組是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
b.2020年第一季度![]() 數據在這一組的是:4.6 4.9 5.0 5.1 5.3 5.4 6.3 7.4 7.5 7.8 7.8
數據在這一組的是:4.6 4.9 5.0 5.1 5.3 5.4 6.3 7.4 7.5 7.8 7.8
c.30個省區市2020年第一季度及2019年![]() 增速排名統計圖,如圖2:
增速排名統計圖,如圖2:
d.北京2020年第一季度![]() 數據約為7.5千億,
數據約為7.5千億,![]() 增速排名為第22.
增速排名為第22.
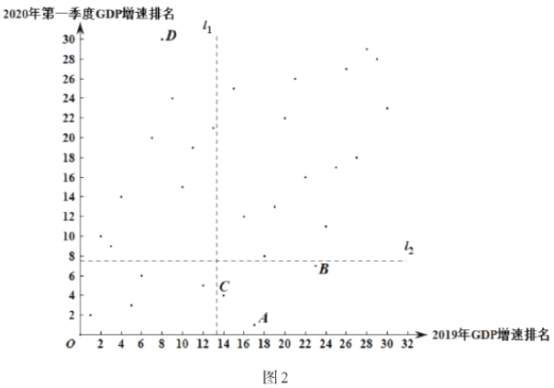
根據以上信息,回答下列問題:
(1)在30個省區市中,北京2020年第一季度![]() 的數據排名第______.
的數據排名第______.
(2)在30個省區市2020年第一季度及2019年![]() 增速排名統計圖中,請在圖中用“○”圈出代表北京的點.
增速排名統計圖中,請在圖中用“○”圈出代表北京的點.
(3)2020年第一季度![]() 增速排名位于北京之后的幾個省份中,2019年
增速排名位于北京之后的幾個省份中,2019年![]() 增速排名的最好成績是第_______.
增速排名的最好成績是第_______.
(4)下列推斷合理的是___________.
①與2019年![]() 增速排名相比,在疫情沖擊下,2020年全國第一季度增速排名,部分省市有較大下滑,如D代表的湖北排名下滑最多.
增速排名相比,在疫情沖擊下,2020年全國第一季度增速排名,部分省市有較大下滑,如D代表的湖北排名下滑最多.
②A、B、C分別代表的新疆、廣西、青海位于西部地區,多為人口凈流出或少量凈流入,經濟發展主要依靠本地勞動力供給,疫后復工復產效率相對較高,相對于2019年![]() 增速排名位置靠前.
增速排名位置靠前.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】垃圾的分類處理與回收利用,可以減少污染,節省資源.深圳市環境衛生局為了提高宣傳實效,抽樣調查了部分居民小區一段時間內生活垃圾的分類情況,其相關信息如下:
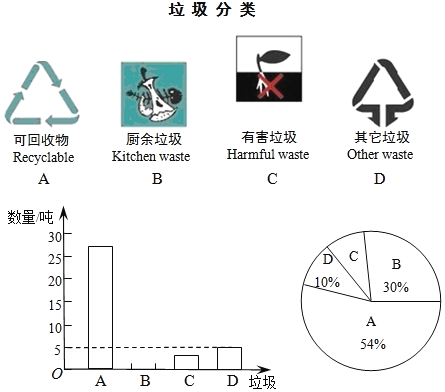
根據圖表解答下列問題:
(1)請將條形統計圖補充完整;
(2)在扇形統計圖中,產生的有害垃圾C所對應的圓心角為 度;
(3)調查發現,在可回收物中塑料類垃圾占13%,每回收1噸塑料類垃圾可獲得0.5噸二級原料.假設深圳市每天產生的生活垃圾為28500噸,且全部分類處理,那么每天回收的塑料類垃圾可以獲得多少噸二級原料?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,以斜邊AB上的中線CD為直徑作⊙O,分別與AC,BC交于點E,F. 過點F作⊙O的切線交AB于點M.
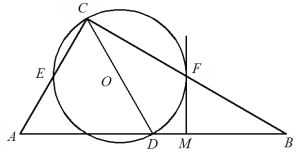
(1)求證:MF⊥AB;
(2)若⊙O的直徑是6,填空:
①連接OF,OM,當FM= 時,四邊形OMBF是平行四邊形;
②連接DE,DF,當AC= 時,四邊形CEDF是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校七年級有學生400人,為了解這個年級普及安全教育的情況,隨機抽取了20名學生,進行安全教育考試,測試成績(百分制)如下:
71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
(1)請補全七年級20名學生安全教育測試成績頻數分布直方圖;
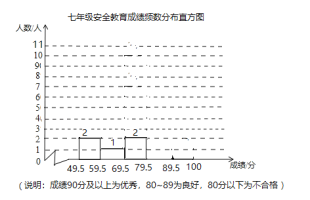
(2)樣本數據的平均數、中位數、眾數、優秀率如下表所示,請補充完整;
年級 | 平均數 | 中位數 | 眾數 | 優秀率 |
七年級 | 85.4 |
|
|
|
(3)估計七年級成績優秀的學生人數約為_________人.
(4)學校有安全教育老師男女各2名,現從這4名老師中隨機挑選2名參加“安全教育”宣傳活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
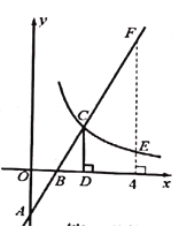
【題目】如圖,在平面直角坐標系中,直線![]() 與坐標軸交于
與坐標軸交于![]() 兩點,與雙曲線
兩點,與雙曲線![]() 交于點
交于點![]() , 過點
, 過點![]() 作
作![]() 軸,且
軸,且![]() ,則以下結論錯誤的是( )
,則以下結論錯誤的是( )
A.![]()
B.當![]() 時,
時,![]()
C.當![]() 時,
時,![]()
D.當![]() 時,
時,![]() 隨
隨![]() 的增大而增大,
的增大而增大,![]() 隨
隨![]() 的增大而減小
的增大而減小
查看答案和解析>>
科目:初中數學 來源: 題型:
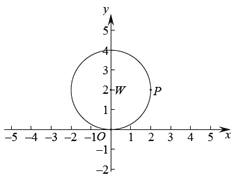
【題目】如圖,在平面直角坐標系![]() 中,存在半徑為2,圓心為(0,2)的
中,存在半徑為2,圓心為(0,2)的![]() ,點
,點![]() 為
為![]() 上的任意一點,線段
上的任意一點,線段![]() 繞點
繞點![]() 逆時針旋轉90°得到線段
逆時針旋轉90°得到線段![]() ,如果點
,如果點![]() 在線段
在線段![]() 上,那么稱點
上,那么稱點![]() 為
為![]() 的“限距點”.
的“限距點”.
(1)在點![]() 中,
中,![]() 的“限距點”為____________________________;
的“限距點”為____________________________;
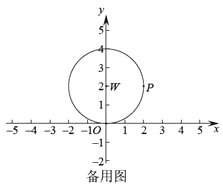
(2)如果過點![]() 且平行于
且平行于![]() 軸的直線
軸的直線![]() 上始終存在
上始終存在![]() 的“限距點”,畫出示意圖并直接寫出
的“限距點”,畫出示意圖并直接寫出![]() 的取值范圍;
的取值范圍;
(3)![]() 的圓心為
的圓心為![]() ,半徑為1,如果
,半徑為1,如果![]() 上始終存在
上始終存在![]() 的“限距點”,請直接寫出
的“限距點”,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩位同學進校時需要從學校大門A、B、C三個入口處中的任意一處測量體溫,體溫正常方可進校.
(1)甲同學在A入口處測量體溫的概率是 ;
(2)求甲、乙兩位同學在同一入口處測量體溫的概率.(用“畫樹狀圖”或“列表”的方法寫出分析過程)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com