
【題目】如圖,數軸上點A對應的有理數為20,點P以每秒2個單位長度的速度從點A出發,點Q以每秒4個單位長度的速度從原點O出發,且P,Q兩點同時向數軸正方向運動,設運動時間為t秒. ![]()
(1)當t=2時,P,Q兩點對應的有理數分別是 , , PQ=;
(2)當PQ=10時,求t的值.
【答案】
(1)24;8;16
(2)解:①當點P在點Q右側時,
PQ=(20+2t)﹣4t=10,
解得:t=5;
②當點P在點Q左側時,
PQ=4t﹣(20+2t)=10,
解得:t=15.
綜上所述,t的值為5秒或15秒
【解析】解:(1)∵20+2×2=24,4×2=8, ∴當t=2時,P,Q兩點對應的有理數分別是24,8,
∴PQ=24﹣8=16.
所以答案是:24;8;16.
【考點精析】關于本題考查的數軸和代數式求值,需要了解數軸是規定了原點、正方向、單位長度的一條直線;求代數式的值,一般是先將代數式化簡,然后再將字母的取值代入;求代數式的值,有時求不出其字母的值,需要利用技巧,“整體”代入才能得出正確答案.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:
【題目】用作位似形的方法,可以將一個圖形放大或縮小,位似中心( )
A.只能選在原圖形的外部
B.只能選在原圖形的內部
C.只能選在原圖形的邊上
D.可以選擇任意位置
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某市第四次黨代會上,提出了建設美麗城市決勝全面小康的奮斗目標,為策應市委號召,學校決定改造校園內的一小廣場,如圖是該廣場的平面示意圖,它是由6個正方形拼成的長方形,已知中間最小的正方形A的邊長是1米. 
(1)若設圖中最大正方形B的邊長是x米,請用含x的代數式分別表示出正方形F、E和C的邊長;
(2)觀察圖形的特點可知,長方形相對的兩邊是相等的(如圖中的MN和PQ).請根據這個等量關系,求出x的值;
(3)現沿著長方形廣場的四條邊鋪設下水管道,由甲、乙2個工程隊單獨鋪設分別需要10天、15天完成.兩隊合作施工2天后,因甲隊另有任務,余下的工程由乙隊單獨施工,試問還要多少天完成?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校要求八年級同學在課外活動中,必須在五項球類(籃球、足球、排球、羽毛球、乒乓球)活動中任選一項(只能選一項)參加訓練,為了了解八年級學生參加球類活動的整體情況,現以八年級2班作為樣本,對該班學生參加球類活動的情況進行統計,并繪制了如圖所示的不完整統計表和扇形統計圖:

根據圖中提供的信息,解答下列問題:
(1)a= ,b= ;
(2)該校八年級學生共有600人,則該年級參加足球活動的人數約 人;
(3)該班參加乒乓球活動的5位同學中,有3位男同學(A,B,C)和2位女同學(D,E),現準備從中選取兩名同學組成雙打組合,用樹狀圖或列表法求恰好選出一男一女組成混合雙打組合的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D為BC的中點,若動點E以1cm/s的速度從A點出發,沿著A→B→A的方向運動,設E點的運動時間為t秒,連接DE,當△BDE是直角三角形時,t的值______________.
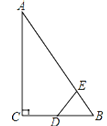
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】能斷定A,B,C三點共線的是( )
A. AB=6,AC=2,BC=5B. AB=6,AC=2,BC=4
C. AB=6,AC=3,BC=4D. AB=6,AC=5,BC=4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com