
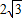 ,0)作圓B的切線交圓于點P,已知tan∠PAB=
,0)作圓B的切線交圓于點P,已知tan∠PAB=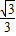 ,拋物線C經過A,P兩點.
,拋物線C經過A,P兩點.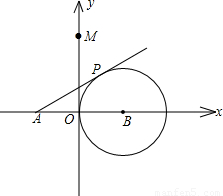
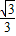 ,
,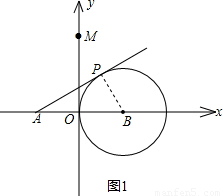
 (OA+OB)=
(OA+OB)= (2
(2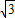 +r),
+r), .
.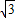 cos60°,2
cos60°,2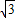 sin60°),
sin60°),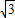 ,3)
,3)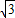 ,3),(2
,3),(2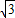 ,0),代入,
,0),代入,
 x2+4
x2+4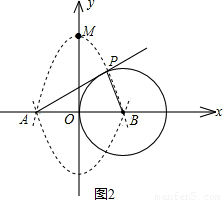
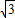 ,-3)
,-3) x2-4
x2-4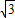 ,3),A點坐標為(-2
,3),A點坐標為(-2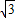 ,0),M點坐標為(0,t).
,0),M點坐標為(0,t).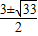 ;
;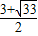 ),(0,
),(0,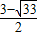 ).
).

 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:
 P,使S四邊形POCA=S△AOB?若存在,請直接寫出點P的坐標;若不存在,請簡要說明理由.
P,使S四邊形POCA=S△AOB?若存在,請直接寫出點P的坐標;若不存在,請簡要說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:
 已如:如圖,在直角坐標系中,以y軸上的點C為圓心,2為半徑的圓與x軸相切于原點O,AB為⊙C的直徑,PA切⊙O于點A,交x軸的負半軸于點P,連接PC交OA于點D.
已如:如圖,在直角坐標系中,以y軸上的點C為圓心,2為半徑的圓與x軸相切于原點O,AB為⊙C的直徑,PA切⊙O于點A,交x軸的負半軸于點P,連接PC交OA于點D.查看答案和解析>>
科目:初中數學 來源:2008-2009學年浙江省臺州市五校第二次聯考九年級(上)月考數學試卷(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2001年全國中考數學試題匯編《圓》(05)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2001年全國中考數學試題匯編《一次函數》(02)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com