【題目】某市開展一項自行車旅游活動，線路需經A、B、C、D四地，如圖，其中A、B、C三地在同一直線上，D地在A地北偏東30°方向，在C地北偏西45°方向，C地在A地北偏東75°方向．且BC=CD=20km，問沿上述線路從A地到D地的路程大約是多少？（最后結果保留整數，參考數據：sin15°≈0.25，cos15°≈0.97，tan15°≈0.27， 
）
【答案】解：由題意可知∠DCA=180°﹣75°﹣45°=60°，
∵BC=CD，
∴△BCD是等邊三角形．
過點B作BE⊥AD，垂足為E，如圖所示：
由題意可知∠DAC=75°﹣30°=45°，
∵△BCD是等邊三角形，
∴∠DBC=60° BD=BC=CD=20km，
∴∠ADB=∠DBC﹣∠DAC=15°，
∴BE=sin15°BD≈0.25×20≈5m，
∴AB= 
= 
≈7m，
∴AB+BC+CD≈7+20+20≈47m．
答：從A地跑到D地的路程約為47m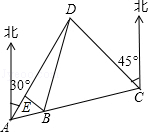
【解析】求出∠DCA的度數，再判斷出BC=CD，據此即可判斷出△BCD是等邊三角形．過點B作BE⊥AD，垂足為E，求出∠DAC的度數，利用三角函數求出AB的長，從而得到AB+BC+CD的長．
中考解讀考點精練系列答案科目：初中數學 來源： 題型：
【題目】如圖所示，火車站、碼頭分別位于A，B兩點，直線a和b分別表示鐵路與河流．
（1）從火車站到碼頭怎樣走最近，畫圖并說明理由；
（2）從碼頭到鐵路怎樣走最近，畫圖并說明理由；
（3）從火車站到河流怎樣走最近，畫圖并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀材料后解決問題：
小明遇到下面一個問題：
計算（2+1）（22+1）（24+1）（28+1）．
經過觀察，小明發現如果將原式進行適當的變形后可以出現特殊的結構，進而可以應用平方差公式解決問題，具體解法如下：（2+1）（22+1）（24+1）（28+1）
=（2+1）（2﹣1）（22+1）（24+1）（28+1）
=（22﹣1）（22+1）（24+1）（28+1）
=（24﹣1）（24+1）（28+1）
=（28﹣1）（28+1）
=216﹣1
請你根據小明解決問題的方法，試著解決以下的問題：
（1）（2+1）（22+1）（24+1）（28+1）（216+1）=_____．
（2）（3+1）（32+1）（34+1）（38+1）（316+1）=_____．
（3）化簡：（m+n）（m2+n2）（m4+n4）（m8+n8）（m16+n16）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=ax2+bx+1（a＜0）的圖象過點（1，0）和（x1 ， 0），且﹣2＜x1＜﹣1，下列5個判斷中：①b＜0；②b﹣a＜0；③a＞b﹣1；④a＜﹣ 
；⑤2a＜b+ ，正確的是（ ）
A.①③
B.①②③
C.①②③⑤
D.①③④⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某出租車從停車場出發，沿著東西向的大街行駛，到晚上6時，一天的行駛記錄如下：（向東行駛記為正，向西行駛記為負，單位：千米）－4、＋7、－9、＋8、＋6、－4、－3、＋12
（1）到晚上6時，出租車在什么位置？
（2）若汽車每千米耗油0.2升，則從停車場出發到晚上6時，出租車共耗油多少升？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知直線AB：y=
x+
分別交x軸、y軸于點B、A兩點,C（3，0），D、E分別為線段AO和線段AC上一動點，BE交y軸于點H,且AD＝CE．當BD＋BE的值最小時，則H點的坐標為（ ）
A. （0，4） B. （0，5） C. （0，
） D. （0，）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小宇想測量位于池塘兩端的A、B兩點的距離．他沿著與直線AB平行的道路EF行走，當行走到點C處，測得∠ACF=45°，再向前行走100米到點D處，測得∠BDF=60°．若直線AB與EF之間的距離為60米，求A、B兩點的距離．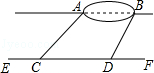 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
