
【題目】如圖,一次函數y=kx+b(k≠0)的圖象過點P(﹣![]() ,0),且與反比例函數
,0),且與反比例函數![]() (m≠0)的圖象相交于點A(﹣2,1)和點B.
(m≠0)的圖象相交于點A(﹣2,1)和點B.
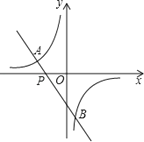
(1)求一次函數和反比例函數的解析式;
(2)求點B的坐標,并根據圖象回答:當x在什么范圍內取值時,一次函數的函數值小于反比例函數的函數值?
【答案】(1)一次函數的解析式為y=﹣2x﹣3,反比例函數的解析式為y=﹣![]() ;
;
(2)當﹣2<x<0或x>![]() 時,一次函數的函數值小于反比例函數的函數值.
時,一次函數的函數值小于反比例函數的函數值.
【解析】
(1)根據待定系數法,可得函數解析式;
(2)根據二元一次方程組,可得函數圖象的交點,根據一次函數圖象位于反比例函數圖象的下方,可得答案.
解:(1)一次函數y=kx+b(k≠0)的圖象過點P(![]() ,0)和A(﹣2,1),
,0)和A(﹣2,1),
∴ ,解得
,解得![]() ,
,
∴一次函數的解析式為y=﹣2x﹣3,
反比例函數y=![]() (m≠0)的圖象過點A(﹣2,1),
(m≠0)的圖象過點A(﹣2,1),
∴![]() ,解得m=﹣2,
,解得m=﹣2,
∴反比例函數的解析式為y=﹣![]() ;
;
(2)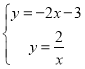 ,解得
,解得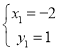 ,或
,或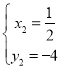 ,
,
∴B(![]() ,﹣4)
,﹣4)
由圖象可知,當﹣2<x<0或x>![]() 時,一次函數的函數值小于反比例函數的函數值.
時,一次函數的函數值小于反比例函數的函數值.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】操作:在△ABC中,AC=BC=4,∠C=90°,將一塊直角三角板的直角頂點放在斜邊AB的中點P處,將三角板繞點P旋轉,三角板的兩直角邊分別交射線AC、CB于D、E兩點。如圖①、②、③是旋轉三角板得到的圖形中的3種情況。
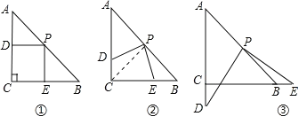
探究:
(1)如圖①,PD⊥AC于D,PE⊥BC于E,則重疊部分四邊形DCEP的面積為___,周長___.
(2)三角板繞點P旋轉,觀察線段PD與PE之間有什么數量關系?并結合圖②加以證明;
(3)三角板繞點P旋轉,△PBE是否能成為等腰三角形?若能,指出所有情況(即寫出△PBE為等腰三角形時CE的長);若不能,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為宣傳普及新冠肺炎防治知識,引導學生做好防控.某校舉行了主題為“防控新冠,從我做起”的線上知識競賽活動,測試內容為20道判斷題,每道題5分,滿分100分.為了解八、九年級學生此次競賽成績的情況,分別隨機在八、九年級各抽取了20名參賽學生的成績.已知抽查得到的八年級的數據如下:
80,95,75,75,90,75,80,65,80,85,75,65,70,65,85,70,95,80,75,80.
為了便于分析數據,統計員對八年級數據進行了整理,得到了表一:
成績等級 | 分數(單位:分) | 學生數 |
|
| 5 |
|
|
|
|
|
|
|
| 2 |
八、九年級成績的平均數、中位數、優秀率如下:(分數80分以上、不含80分為優秀)
年級 | 平均數 | 中位數 | 優秀率 |
八年級 | 77.5 |
|
|
九年級 | 76 | 82.5 | 50% |
(1)根據題目信息填空:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)八年級王宇和九年級程義的分數都為80分,請判斷王宇、程義在各自年級的排名哪位更靠前?請簡述你的理由;
(3)八年級被抽取的20名學生中,獲得![]() 等和
等和![]() 等的學生將被隨機選出2名,協助學校普及新冠肺炎防控知識,求這兩人都為
等的學生將被隨機選出2名,協助學校普及新冠肺炎防控知識,求這兩人都為![]() 等的概率.
等的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著人們生活水平的提高,家用轎車越來越多地進入家庭.王先生家中買了一輛小轎車,他連續記錄了7天中每天行駛的路程(如下表),以50km為標準,多于50km的記為“+”,不足50km的記為“﹣”,剛好50km的記為“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +15 |
(1)王先生這七天中平均每天駕車行駛多少千米?
(2)若每行駛1km需用汽油0.1升,汽油價格為6.5元/升,則王先生家一個月(按30天計)的汽油費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于(x1,0),且﹣1<x1<0,對稱軸x=1.如圖所示,有下列5個結論:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的實數).其中所有結論正確的是______(填寫番號).
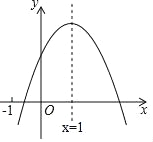
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校學生對《最強大腦》、《朗讀者》、《中國詩詞大會》、《出彩中國人》四個電視節目的喜愛情況,隨杋抽取了![]() 名學生進行調查統計(要求每名學生選出并且只能選出一個自己最喜愛的節目),并將調查結果繪制成如圖統計圖表:
名學生進行調查統計(要求每名學生選出并且只能選出一個自己最喜愛的節目),并將調查結果繪制成如圖統計圖表:
學生最喜愛的節目人數統計表
節目 | 人數(名) | 百分比 |
最強大腦 | 5 | 10% |
朗讀者 | 15 | |
中國詩詞大會 |
| 40% |
出彩中國人 | 10 | 20% |
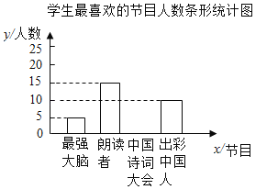
根據以上信息,回答下列問題:
(1)![]() ,
,![]() ;
;
(2)補全上面的條形統計圖;
(3)若該校共有學生![]() 名,估計該校學生最喜愛《朗讀者》節目的人數.
名,估計該校學生最喜愛《朗讀者》節目的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新交通法規實施以來,為了解某社區居民遵守交通法規情況,小明隨機選取部分居民就“行人闖紅燈現象”進行問卷調查,調查分為“A:從不闖紅燈;B:偶爾闖紅燈;C:經常闖紅燈;D:其他”四種情況,并根據調查結果繪制出部分條形統計圖(如圖1)和部分扇形統計圖(如圖2).請根據圖中信息,解答下列問題:
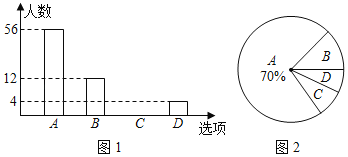
(1)本次調查共選取 名居民;
(2)求出扇形統計圖中“C”所對扇形的圓心角是 度,并將條形統計圖補充完整;
(3)如果該社區共有居民2600人,估計有多少人從不闖紅燈?(請計算說明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知拋物線y=x2﹣mx+n.
(1)當m=2時,
①求拋物線的對稱軸,并用含n的式子表示頂點的縱坐標;
②若點A(﹣2,y1),B(x2,y2)都在拋物線上,且y2>y1,則x2的取值范圍是 ;
(2)已知點P(﹣1,2),將點P向右平移4個單位長度,得到點Q.當n=3時,若拋物線與線段PQ恰有一個公共點,結合函數圖象,求m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com