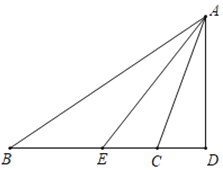
【題目】如圖，△ABC中，∠ACB＞90°，AE平分∠BAC，AD⊥BC交BC的延長線于點D．
（1）若∠B＝30°，∠ACB＝100°，求∠EAD的度數；
（2）若∠B＝α，∠ACB＝β，試用含α、β的式子表示∠EAD．
【答案】（1）
，（2）
．
【解析】
（1）根據垂直的定義得到∠D＝90°，根據鄰補角的定義得到∠ACD
，根據三角形的內角和得到∠BAC＝50°，根據角平分線的定義得到∠CAE
∠BAC＝25°，于是得到結論； （2）根據垂直的定義得到∠D＝90°，得到∠ACD＝
，求得∠BAC
，根據角平分線的定義得到∠CAE∠BAC
，根據角的和差即可得到結論．
解：（1）∵AD⊥BC， ∴∠D＝90°，
∵∠ACB＝100°， ∴∠ACD，
∴∠CAD＝
， ∵∠B＝30°，
∴∠BAD
， ∴∠BAC＝50°，
∵AE平分∠BAC， ∴∠CAE∠BAC＝25°，
∴∠EAD＝∠CAE+∠CAD＝35°；
（2）∵AD⊥BC， ∴∠D＝90°，
∵∠ACB＝β， ∴∠ACD＝，
∴∠CAD
，
∵∠B＝α， ∴∠BAD＝
，
∴∠BAC
，
∵AE平分∠BAC， ∴∠CAE∠BAC，
∴∠EAD＝∠CAE+∠CAD＝
．
智趣寒假作業云南科技出版社系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知直線AB∥CD，直線L和直線AB，CD分別交于點E，F，直線L上有一動點P．
（1）如圖1，點P在E，F之間運動時，∠PMB，∠MPN，∠PND之間有什么關系，并說明理由；
（2）若點P在E，F兩點外側運動時，如圖2和圖3（P點與E，F不重合），試直接寫出∠PMB，∠MPN，∠PND之間有什么關系，不必寫理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，P、Q分別是BC、AC上的點，作PR⊥AB，PS⊥AC，垂足分別是R、S，若AQ=PQ，PR=PS，下面四個結論：①AS=AR；②QP∥AR；③△BRP≌△QSP；④AP垂直平分RS．其中正確結論的序號是（ ）．
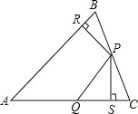
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在探索三角形全等的條件時，老師給出了定長線段
，且長度為
的邊所對的角為
小明和小亮按照所給條件分別畫出了圖1中的三角形，他們把兩個三角形重合在一起（如圖2），其中
發現它們不全等，但他們對該圖形產生了濃厚興趣，并進行了進一步的探究：
（1）當
時（如圖2），小明測得
，請根據小明的測量結果，求
的大小；
（2）當
時，將
沿
翻折，得到
（如圖3），小明和小亮發現
的大小與角度
有關，請找出它們的關系，并說明理由；
（3）如圖4，在（2）問的基礎上，過點
作
的垂線，垂足為點
，延長
到點
，使得
，連接
，請判斷
的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
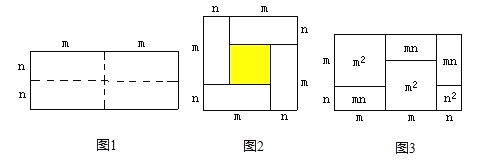
【題目】如圖1是一個長為2m、寬為2n的長方形，沿圖中虛線用剪刀平均分成四塊小長方形，然后按圖2的形狀拼成一個正方形．
（1）圖2中間的小正方形(即陰影部分)面積可表示為________________．
（2）觀察圖2，請你寫出三個代數式(m＋n)2，(m－n)2，mn之間的等量關系式：______________．
（3）根據（2）中的結論，若x＋y=－6，xy=2.75，則x－y=____________．
（4）有許多代數恒等式可以用圖形的面積來表示．如圖3所示，它表示了(2m＋n)(m＋n)=2m2＋3mn＋n2．試畫出一個幾何圖形，使它的面積能表示為(m＋n)(m＋2n)=m2＋3mn＋2n2．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD紙片中，已知∠A=160°，∠B=30°，∠C=60°，四邊形ABCD紙片分別沿EF，GH，OP，MN折疊，使A與A′、B與B′、C與C′、D與D′重合，則∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是（ ）
A. 600° B. 700° C. 720° D. 800°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】問題：如圖①，在直角三角形
中，
，
于點
，可知
（不需要證明）；
（1）探究：如圖②，
，射線
在這個角的內部，點
、
在
的邊
、
上，且
，
于點
，
于點．證明：
；
（2）證明：如圖③，點、在的邊、上，點
、在內部的射線
上，
、
分別是
、
的外角。已知，
．求證：
；
（3）應用：如圖④，在
中，，
．點在邊
上，
，點、在線段上，．若的面積為15，則
與
的面積之和為________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知，∠ABG為銳角，AH∥BG，點C從點B（C不與B重合）出發，沿射線BG的方向移動，CD∥AB交直線AH于點D，CE⊥CD交AB于點E，CF⊥AD，垂足為F（F不與A重合），若∠ECF＝n°，則∠BAF的度數為_____度．（用n來表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知梯形ABCD中，AD∥BC，AB＝AD(如圖所示)．
(1)在下圖中，用尺規作∠BAD的平分線AE交BC于點E，連接DE(保留作圖痕跡，不寫作法)，并證明四邊形ABED是菱形；
(2)若∠ABC＝60°，EC＝2BE.求證：ED⊥DC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com