
如圖,已知一次函數![]() 的圖象與x軸相交于點A,與反比例函數
的圖象與x軸相交于點A,與反比例函數![]()
的圖象相交于B(-1,5)、C(![]() ,d)兩點.點P(m,n)是一次函數
,d)兩點.點P(m,n)是一次函數![]() 的圖象上的動點.
的圖象上的動點.
(1)求k、b的值;
(2)設![]() ,過點P作x軸的平行線與函數
,過點P作x軸的平行線與函數![]() 的圖象相交于點D.試問△PAD的面積是
的圖象相交于點D.試問△PAD的面積是
否存在最大值?若存在,請求出面積的最大值及此時點P的坐標;若不存在,請說明理由;
(3)設![]() ,如果在兩
,如果在兩![]() 個實數m與n之間(不包括m和n)有且只有一個整數,求實數a的取值
個實數m與n之間(不包括m和n)有且只有一個整數,求實數a的取值
范圍.

解:(1)將點B 的坐標代入![]() ,得
,得![]() ,解得
,解得![]() 。
。
∴反比例函數解析式為![]() 。
。
將點C(![]() ,d)的坐標代入
,d)的坐標代入![]() ,得
,得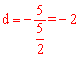 。∴C(
。∴C(![]() ,-2)。
,-2)。
∵一次函數![]() 的圖象經過B(-1,5)、C(
的圖象經過B(-1,5)、C(![]() ,-2)兩點,
,-2)兩點,
∴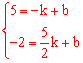 ,解得
,解得![]() 。
。

∵DP∥x軸,且點D在![]() 的圖象上,
的圖象上,
∴![]() ,即D(
,即D(![]() )。
)。
∴△PAD的面積為![]() 。
。
∴S關于n的二次函數的圖象開口向下,有最大值。
又∵n=![]() ,
,![]() ,得
,得![]() ,而
,而![]() 。
。
∴當![]() 時,即P(
時,即P(![]() )時,△PAD的面積S最大,為
)時,△PAD的面積S最大,為![]() 。
。
(3)由已知,P(![]()
![]() )。
)。
易知m≠n,即![]() ,即
,即![]() 。
。
若![]() ,則
,則![]() 。
。
由題設,![]() ,解出不等式組的解為
,解出不等式組的解為![]() 。
。
若![]() ,則
,則![]() 。
。
由題設,![]() ,解出不等式組的解為
,解出不等式組的解為![]() 。
。
綜上所述,數a的取值范圍為![]() ,
,![]() 。
。
【考點】反比例函數和一次函數綜合問題,曲線上點的坐標與方程的關系,平行的性質,二次函數的性質,不等式組的應用。
【分析】(1)根據曲線上點的坐標與方程的關系,由B 的坐標求得![]() ,從而得到
,從而得到![]() ;由點C在
;由點C在![]() 上求得
上求得![]() ,即得點C的坐標;由點B、C在
,即得點C的坐標;由點B、C在![]() 上,得方程組,解出即可求得k、b的值。
上,得方程組,解出即可求得k、b的值。
(2)求出△PAD的面積S關于n的二次函數(也可求出關于m),應用二次函數的最值原理即可求得面積的最大值及此時點P的坐標。
(3)由m≠n得到![]() 。分
。分![]() 和
和![]() 兩種情況求解。
兩種情況求解。


科目:初中數學 來源: 題型:
 在第一象限,CD⊥x軸于D,若OA=OB=OD=1.
在第一象限,CD⊥x軸于D,若OA=OB=OD=1.查看答案和解析>>
科目:初中數學 來源:2013屆山東省濟南市天橋區九年級中考一模數學試卷(帶解析) 題型:解答題
如圖,已知一次函數 的圖象經過
的圖象經過 ,
, 兩點,并且交x軸于點C,交y軸于點D.
兩點,并且交x軸于點C,交y軸于點D.
(1)求該一次函數的解析式;
(2)求 的值;
的值;
(3)求證: .
.
查看答案和解析>>
科目:初中數學 來源:2011——2012學年北京西城實驗學校初二期中數學試卷(帶解析) 題型:解答題
如圖,已知一次函數 的圖象與
的圖象與 軸、
軸、 軸分別交于A、B兩點且與反比例函數
軸分別交于A、B兩點且與反比例函數 的圖象在第一象限交于C點,CD⊥
的圖象在第一象限交于C點,CD⊥ 軸于D點,若∠C A D=
軸于D點,若∠C A D= ,A B =
,A B =  ,C D =
,C D = 

(1) 求點A、B、D的坐標
(2) 求一次函數的解析式
(3) 反比例函數的解析式
(4) 求△BCD的面積
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com