
【題目】已知A(2,y1),B(﹣3,y2),C(﹣5,y3)三個點都在反比例函數![]() 的圖象上,比較y1,y2,y3的大小,則下列各式正確的是( )
的圖象上,比較y1,y2,y3的大小,則下列各式正確的是( )
A.y1<y2<y3B.y2<y3<y1C.y1<y3<y2D.y3<y2<y1
科目:初中數學 來源: 題型:
【題目】已知銳角∠AOB如圖,(1)在射線OA上取一點C,以點O為圓心,OC長為半徑作![]() ,交射線OB于點D,連接CD;
,交射線OB于點D,連接CD;
(2)分別以點C,D為圓心,CD長為半徑作弧,交![]() 于點M,N;
于點M,N;
(3)連接OM,MN.
根據以上作圖過程及所作圖形,下列結論中錯誤的是( )

A. ∠COM=∠CODB. 若OM=MN,則∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1是一輛吊車的實物圖,圖2是其工作示意圖,![]() 是可以伸縮的起重臂,其轉動點
是可以伸縮的起重臂,其轉動點![]() 離地面
離地面![]() 的高度
的高度![]() 為
為![]() .當起重臂
.當起重臂![]() 長度為
長度為![]() ,張角
,張角![]() 為118°.
為118°.
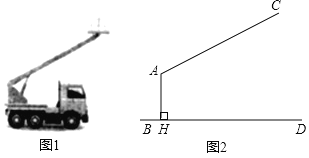
(1)求操作平臺![]() 離地面的高度;
離地面的高度;
(2)當張角![]() 為120°,其它條件不變時,求操作平臺
為120°,其它條件不變時,求操作平臺![]() 升高的高度.
升高的高度.
(最后結果精確到0.1,參考數據:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() 兩點,直線
兩點,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .點
.點![]() 是
是![]() 軸上方的拋物線上一動點,過點
軸上方的拋物線上一動點,過點![]() 作
作![]() 軸于點
軸于點![]() ,交直線
,交直線![]() 于點
于點![]() .設點
.設點![]() 的橫坐標為
的橫坐標為![]() .
.

(1)求拋物線的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若點![]() 是點
是點![]() 關于直線OE的對稱點,是否存在點
關于直線OE的對稱點,是否存在點![]() ,使點
,使點![]() 落在
落在![]() 上?若存在,請直接寫出相應的點
上?若存在,請直接寫出相應的點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于三角函數有如下的公式:
①cos(α+β)=cosαcosβ﹣sinαsinβ;sin(α+β)=sinαcosβ+cosαsinβ;
②tan(α+β)=![]() .
.
③利用這些公式可以將一些不是特殊角的三角函數轉化為特殊角的三角函數來求值,如tan105°=tan(45°+60°)=![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
根據上面的知識,你可以選擇適當的公式解決下面的實際問題:
(1)求cos75°的值;
(2)如圖,直升機在一建筑物CD上方的點A處測得建筑物頂端點D的俯角α為60°,底端點C的俯角β為75°,此時直升機與建筑物CD的水平距離BC為42m,求建筑物CD的高.
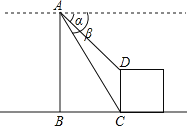
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BM是以AB為直徑的⊙O的切線,B為切點,BC平分∠ABM,弦CD交AB于點E,DE=OE.

(1)求證:△ACB是等腰直角三角形;
(2)求證:OA2=OEDC:
(3)求tan∠ACD的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形![]() 邊長為
邊長為![]() ,
,![]() ,
,![]() 分別為線段
分別為線段![]() ,
,![]() 上一點,且
上一點,且![]() ,
,![]() ,
,![]() 與
與![]() 相交于
相交于![]() ,
,![]() 為線段
為線段![]() 上一點(不與端點重合),
上一點(不與端點重合),![]() 為線段
為線段![]() 上一點(不與端點重合),則
上一點(不與端點重合),則![]() 的最小值為( )
的最小值為( )
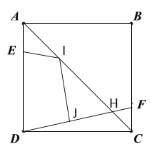
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
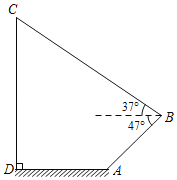
【題目】如圖,一架無人機在距離地面高度為21.4米的點B處,測得地面點A的俯角為47°,接著,這架無人機從點B沿仰角為37°的方向繼續飛行20![]() 米到達點C,此時測得點C恰好在地面點D的正上方,且A,D兩點在同一水平線上,求A,D兩點之間的距離.(結果精確到1米;參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin47°≈0.73,cos47°≈0.68,tan47°≈1.07,
米到達點C,此時測得點C恰好在地面點D的正上方,且A,D兩點在同一水平線上,求A,D兩點之間的距離.(結果精確到1米;參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin47°≈0.73,cos47°≈0.68,tan47°≈1.07,![]() ≈2.45)
≈2.45)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com