【題目】如圖,∠1=65°,∠2=50°,∠3=115°,EG平分∠NEF,
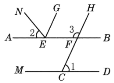
試說明:(1)AB∥CD;
(2)EG∥FH的理由.
【答案】（1）見解析；（2）理由見解析.
【解析】
(1)已知∠3的度數，根據鄰補角定義可以求出∠HFB的度數，與∠1的度數相等，根據同位角相等兩直線平行即可得AB∥CD；
(2)根據角平分線定義可以得出∠GEF=∠NEG，根據平角定義即可求出∠GEF的度數即可得出EG∥FH.
證明：(1)∵∠3=115°，∠3+∠HFB=180°，
∴∠HFB=180°－115°=65°，
∴∠1=∠HFB，
∴AB∥CD；
(2)∵EG平分∠NEF，
∴∠GEF=∠NEG，∠2=50°，
∵∠2+∠NEG+∠GEF=180°，
∴∠GEF=
(180°－∠2)= (180°－50°)=65°.
即∠GEF=∠HFB=65°，
∴EG∥FH.
陽光同學一線名師全優好卷系列答案科目：初中數學 來源： 題型：
【題目】光明中學八年級甲、乙、丙三個班中，每班的學生人數都為40名，某次數學考試的成績統計如圖：(每組分數含最小值，不含最大值)
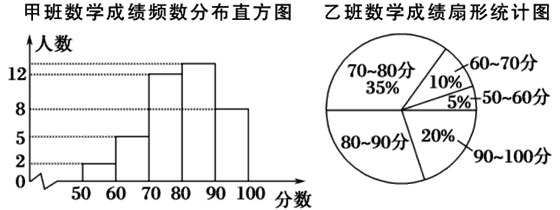
丙班數學成績頻數統計表
分數 | 50～60 | 60～70 | 70～80 | 80～90 | 90～100 |
人數 | 1 | 4 | 15 | 11 | 9 |
根據上圖及統計表提供的信息，則80～90分這一組人數最多的班是________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，AC為對角線，E為AB上一點，過點E作EF∥AD，與AC、DC分別交于點G，F，H為CG的中點，連接DE，EH，DH，FH．下列結論： ①EG=DF；②∠AEH+∠ADH=180°；③△EHF≌△DHC；④若 
= 
，則3S△EDH=13S△DHC ， 其中結論正確的有 ．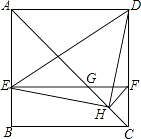 
查看答案和解析>>
科目：初中數學 來源： 題型：
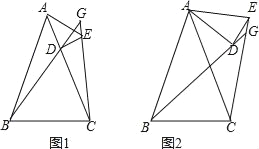
【題目】已知AB=AC，AD=AE，∠BAC=∠DAE，直線BD、CE交于點G，
（1）如圖1，點D在AC上，求證：∠BGC=∠BAC；
（2）如圖2，當點D不在AC上，（1）中的結論還成立嗎？若成立，請證明；若不成立，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知：∠MON=30°，點A1、A2、A3、…在射線ON上，點B1、B2、B3、…在射線OM上，△A1B1A2、△A2B2A3、△A3B3A4、…均為等邊三角形，若OA1=1，則△A9B9A10的邊長為（ ）
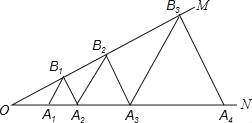
A. 32 B. 64 C. 128 D. 256
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在正方形網格中，每個小正方形的邊長均為1個單位長度，△ABC的三個頂點的位置如圖所示，現將△ABC平移，使點A變換為點A′，點B′、C′分別是B、C的對應點．
（1）請畫出平移后的△A′B′C′，并求△A′B′C′的面積；
（2）若連接AA′，CC′，則這兩條線段之間的關系是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
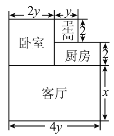
【題目】小王購買了一套經濟適用房，他準備將地面鋪上地磚，地面結構如圖所示，根據圖中的數據(單位：m)，解答下列問題：
(1)用含x的代數式表示地面總面積；
(2)當x＝4，y＝2時，鋪1 m2地磚的平均費用為30元，那么鋪地磚的總費用為多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某地為了鼓勵居民節約用水，決定實行兩級收費制，即每月用水量不超過15噸(含15噸)時，每噸按政府補貼優惠價收費；每月超過15噸時，超過部分每噸按市場調節價收費．小明家1月份用水23噸，交水費35元，2月份用水19噸，交水費25元．
(1)求每噸水的政府補貼優惠價與市場調節價分別是多少；
(2)小明家3月份用水24噸，他家應交水費多少元？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
