
【題目】如圖,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,
兩點,![]() ,交
,交![]() 軸于點
軸于點![]() ,對稱軸是直線
,對稱軸是直線![]() .
.
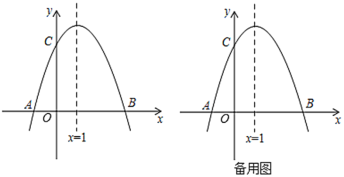
(1)求拋物線的解析式及點![]() 的坐標;
的坐標;
(2)連接![]() ,
,![]() 是線段
是線段![]() 上一點,
上一點,![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 正好落在
正好落在![]() 上,求點
上,求點![]() 的坐標;
的坐標;
(3)動點![]() 從點
從點![]() 出發,以每秒2個單位長度的速度向點
出發,以每秒2個單位長度的速度向點![]() 運動,過
運動,過![]() 作
作![]() 軸的垂線交拋物線于點
軸的垂線交拋物線于點![]() ,交線段
,交線段![]() 于點
于點![]() .設運動時間為
.設運動時間為![]() (
(![]() )秒.若
)秒.若![]() 與
與![]() 相似,請求出
相似,請求出![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
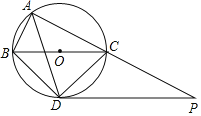
【題目】如圖,⊙O是△ABC的外接圓,點O在BC邊上,∠BAC的平分線交⊙O于點D,連接BD、CD,過點D作BC的平行線與AC的延長線相交于點P.
(1)求證:PD是⊙O的切線;
(2)求證:△ABD∽△DCP;
(3)當AB=5cm,AC=12cm時,求線段PC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在 10×6 的正方形網格中,每個小正方形的邊長均為 1,線段 AB 的端點 A、B 均在小正方形的頂點上.
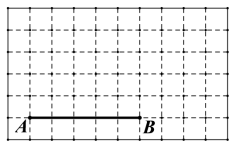
(1)在圖中畫出以 AB 為一腰的等腰△ABC,點 C 在小正方形頂點上,△ABC 為鈍角三角形,且△ABC 的面積為![]() ;
;
(2)在圖中畫出以 AB 為斜邊的直角三角形 ABD, 點 D在小正方形的頂點上,且 AD>BD;
(3)連接 CD,請你直接寫出線段 CD 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以AB為直徑的⊙O交∠BAD的平分線于點C,交AD于點F,過點C作CD⊥AD于D,交AB的延長線于點E.
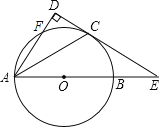
(1)求證:CD為⊙O的切線;
(2)若![]() =
=![]() ,求cos∠DAB的值.
,求cos∠DAB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某童裝專賣店在銷售中發現,一款童裝每件進價為40元,若銷售價為60元,每天可售出20件,為迎接“雙十一”,專賣店決定采取適當的降價措施,以擴大銷售量,經市場調查發現,如果每件童裝降價1元,那么平均可多售出2件![]() 設每件童裝降價x元
設每件童裝降價x元![]() 時,平均每天可盈利y元.
時,平均每天可盈利y元.
![]() 寫出y與x的函數關系式;
寫出y與x的函數關系式;
![]() 當該專賣店每件童裝降價多少元時,平均每天盈利400元?
當該專賣店每件童裝降價多少元時,平均每天盈利400元?
![]() 該專賣店要想平均每天盈利600元,可能嗎?請說明理由.
該專賣店要想平均每天盈利600元,可能嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
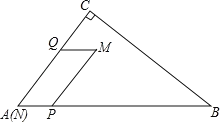
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .點
.點![]() 從點
從點![]() 出發,沿
出發,沿![]() 以每秒1個單位的速度向終點
以每秒1個單位的速度向終點![]() 運動;同時,點
運動;同時,點![]() 從點
從點![]() 出發,沿
出發,沿![]() 以每秒2個單位的速度向終點
以每秒2個單位的速度向終點![]() 運動,當
運動,當![]() 、
、![]() 兩點其中一點到達點
兩點其中一點到達點![]() 時,另一點也隨之停止運動,過點
時,另一點也隨之停止運動,過點![]() 作
作![]() ,過點
,過點![]() 作
作![]() .當點
.當點![]() 與點
與點![]() 不重合時,以
不重合時,以![]() 、
、![]() 為鄰邊作
為鄰邊作![]() .設
.設![]() 、
、![]() 兩點的運動時間為
兩點的運動時間為![]() 秒.
秒.
(1)求線段![]() 的長.(用含
的長.(用含![]() 的代數式表示)
的代數式表示)
(2)點![]() 在邊
在邊![]() 上運動,當點
上運動,當點![]() 落在邊
落在邊![]() 上時,求
上時,求![]() 的值.
的值.
(3)設![]() 與
與![]() 重疊部分圖形的面積為
重疊部分圖形的面積為![]() ,當點
,當點![]() 在
在![]() 內部時,求
內部時,求![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
(4)當![]() 的一邊是它鄰邊2倍時,直接寫出
的一邊是它鄰邊2倍時,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
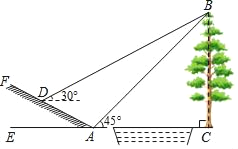
【題目】如圖所示,某數學活動小組選定測量小河對岸大樹BC的高度,他們在斜坡AF上的D處測得大樹頂端B的仰角是30°,在地面上A處測得大樹頂端B的仰角是45°.若坡角∠FAE=30°,AD=6m,求大樹的高度.(結果保留整數,參考數據:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B、C三瓶不同濃度的酒精,A瓶內有酒精2kg,濃度x%,B瓶有酒精3kg,濃度y%,C瓶有酒精5kg,濃度z%,從A瓶中倒出10%,B瓶中倒出20%,C瓶中倒出24%,混合后測得濃度33.5%,將混合后的溶液倒回瓶中,使它們恢復原來的質量,再從A瓶倒出30%,B瓶倒出30%,C瓶倒出30%,混合后測得濃度為31.5%,測量發現![]() ,
,![]() ,
,![]() ,且x、y、z均為整數,則把起初A、B兩瓶酒精全部混合后的濃度為______.
,且x、y、z均為整數,則把起初A、B兩瓶酒精全部混合后的濃度為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
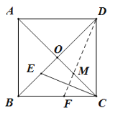
【題目】如圖,邊長為2的正方形ABCD的對角線AC與BD交于點O,將正方形ABCD沿DF直線折疊,點C落在對角線BD上的點E處,折痕DF交AC于點M,則OM的長為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com