
【題目】在等邊△ABC中:
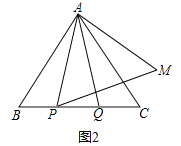
(1)如圖1,P,Q是BC邊上的兩點,AP=AQ,∠BAP=20°,求∠AQB的度數;
(2)點P,Q是BC邊上的兩個動點(不與點B,C重合),點P在點Q的左側,且AP=AQ,點Q關于直線AC的對稱點為M,連接AM,PM.
①依題意將圖2補全;
②小茹通過觀察、實驗提出猜想:在點P,Q運動的過程中,始終有PA=PM,小茹把這個猜想與同學們進行交流,通過討論,形成了證明該猜想的幾種想法:
想法1:要證明PA=PM,只需證△APM是等邊三角形;
想法2:在BA上取一點N,使得BN=BP,要證明PA=PM,只需證△ANP≌△PCM;
想法3:將線段BP繞點B順時針旋轉60°,得到線段BK,要證PA=PM,只需證PA=CK,PM=CK…
請你參考上面的想法,幫助小茹證明PA=PM(一種方法即可).

【答案】(1)40°;(2)①作圖見解析;②證明見解析.
【解析】
試題分析:(1)根據等腰三角形的性質得到∠APQ=∠AQP,由鄰補角的定義得到∠APB=∠AQC,根據三角形外角的性質即可得到結論;
(2)①根據要求作出圖形,如圖2;
②根據等腰三角形的性質得到∠APQ=∠AQP,由鄰補角的定義得到∠APB=∠AQC,由點Q關于直線AC的對稱點為M,得到AQ=AM,∠OAC=∠MAC,等量代換得到∠MAC=∠BAP,推出△APM是等邊三角形,根據等邊三角形的性質即可得到結論.
試題解析:(1)∵AP=AQ,∴∠APQ=∠AQP,∴∠APB=∠AQC,∵△ABC是等邊三角形,∴∠B=∠C=60°,∴∠BAP=∠CAQ=20°,∴∠PAQ=∠BAC﹣∠BAP﹣∠CAQ=60°﹣20°﹣20°=20°,∴∠BAQ=∠BAP+∠PAQ=40°;
(2)①如圖2;
②∵AP=AQ,∴∠APQ=∠AQP,∴∠APB=∠AQC,∵△ABC是等邊三角形,∴∠B=∠C=60°,∴∠BAP=∠CAQ,∵點Q關于直線AC的對稱點為M,∴AQ=AM,∠QAC=∠MAC,∴∠MAC=∠BAP,∴∠BAP+∠PAC=∠MAC+∠CAP=60°,∴∠PAM=60°,∵AP=AQ,∴AP=AM,∴△APM是等邊三角形,∴AP=PM.


科目:初中數學 來源: 題型:
【題目】如圖,A是數軸上表示-30的點,B是數軸上表示10的點,C是數軸上表示18的點,點A,B,C在數軸上同時向數軸的正方向運動,點A運動的速度是6個單位長度每秒,點B和C運動的速度是3個單位長度每秒.設三個點運動的時間為t秒(t≠5),設線段OA的中點為P,線段OB的中點為M,線段OC的中點為N,當2PM-PN=2時,t的值為_____.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分8分)某種電子產品共![]() 件,其中有正品和次品.已知從中任意取出一件,取得的產品為次品的概率為
件,其中有正品和次品.已知從中任意取出一件,取得的產品為次品的概率為![]() .
.
(1)該批產品有正品 件;
(2)如果從中任意取出![]() 件,利用列表或樹狀圖求取出
件,利用列表或樹狀圖求取出![]() 件都是正品的概率.
件都是正品的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,點P的坐標為(![]() ,
,![]() ),點Q的坐標為(
),點Q的坐標為(![]() ,
,![]() ),且
),且![]() ,
,![]() ,若P,Q為某個矩形的兩個頂點,且該矩形的邊均與某條坐標軸垂直,則稱該矩形為點P,Q的“相關矩形”.下圖為點P,Q 的“相關矩形”的示意圖.
,若P,Q為某個矩形的兩個頂點,且該矩形的邊均與某條坐標軸垂直,則稱該矩形為點P,Q的“相關矩形”.下圖為點P,Q 的“相關矩形”的示意圖.
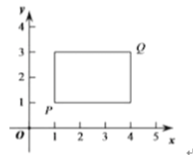
(1)已知點A的坐標為(1,0).
①若點B的坐標為(3,1)求點A,B的“相關矩形”的面積;
②點C在直線x=3上,若點A,C的“相關矩形”為正方形,求直線AC的表達式;
(2)⊙O的半徑為![]() ,點M的坐標為(m,3).若在⊙O上存在一點N,使得點M,N的“相關矩形”為正方形,求m的取值范圍.
,點M的坐標為(m,3).若在⊙O上存在一點N,使得點M,N的“相關矩形”為正方形,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】調查作業:了解你所住小區家庭5月份用氣量情況.
小天、小東和小蕓三位同學住在同一小區,該小區共有300戶家庭,每戶家庭人數在2-5之間,這300戶家庭的平均人數均為3.4.
小天、小東、小蕓各自對該小區家庭5月份用氣量情況進行了抽樣調查,將收集的數據進行了整理,繪制的統計表分別為表1、表2和表3.
表1 抽樣調查小區4戶家庭5月份用氣量統計表 (單位:![]() )
)

表2 抽樣調查小區15戶家庭5月份用氣量統計表 (單位:![]() )
)

表3 抽樣調查小區15戶家庭5月份用氣量統計表 (單位:![]() )
)

根據以上材料回答問題:
小天、小東和小蕓三人中,哪一位同學抽樣調查的數據能較好地反映出該小區家庭5月份用氣量情況,并簡要說明其他兩位同學抽樣調查地不足之處.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解茂名某水果批發市場荔枝的銷售情況,某部門對該市場的三種荔枝品種A、B、C在6月上半月的銷售進行調查統計,繪制成如下兩個統計圖(均不完整).請你結合圖中的信息,解答下列問題:
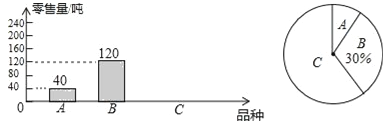
(1)該市場6月上半月共銷售這三種荔枝多少噸?
(2)該市場某商場計劃六月下半月進貨A、B、C三種荔枝共500千克,根據該市場6月上半月的銷售情況,求該商場應購進C品種荔枝多少千克比較合理?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com