Question

【題目】如圖，△ABC是邊長為6的等邊三角形，P是AC邊上一動點，由A向C運動（與A、C不重合），Q是CB延長線上一點，與點P同時以相同的速度由B向CB延長線方向運動（Q不與B重合），過P作PE⊥AB于E，連接PQ交AB于D．

（Ⅰ）若設AP＝x，則PC＝　 　，QC＝　 　；（用含x的代數式表示）

（Ⅱ）當∠BQD＝30°時，求AP的長；

（Ⅲ）在運動過程中線段ED的長是否發生變化？如果不變，求出線段ED的長；如果變化請說明理由．

Answer 1

【答案】（Ⅰ）6﹣x，6+x；（Ⅱ）2；（Ⅲ）線段DE的長度不會改變.DE=3

【解析】

(1)根據等邊三角形的性質可知AB＝BC＝AC＝6，然后根據題意解答即可;

（2）在（1）的基礎上，再利用直角三角形30°所對的邊等于斜邊的一半進行解答即可.

(3) 作QF⊥AB，交直線AB的延長線于點F，連接QE，PF;根據題意和等邊三角形的性質證明△APE≌△BQF（AAS），進一步說明四邊形PEQF是平行四邊形，最后說明DE＝AB，即可說明DE的長度不變.

解：（Ⅰ）∵△ABC是邊長為6的等邊三角形，

∴AB＝BC＝AC＝6，

設AP＝x，則PC＝6﹣x，QB＝x，

∴QC＝QB+BC＝6+x，

故答案為：6﹣x，6+x；

（Ⅱ）

∵在Rt△QCP中，∠BQD＝30°，

∴PC＝QC，即6﹣x＝（6+x），解得x＝2，

∴AP＝2；

（Ⅲ）當點P、Q運動時，線段DE的長度不會改變．理由如下：

作QF⊥AB，交直線AB的延長線于點F，連接QE，PF，

又∵PE⊥AB于E，

∴∠DFQ＝∠AEP＝90°，

∵點P、Q速度相同，

∴AP＝BQ，

∵△ABC是等邊三角形，

∴∠A＝∠ABC＝∠FBQ＝60°，

在△APE和△BQF中，

∵∠AEP＝∠BFQ＝90°，

∴∠APE＝∠BQF，

∴在△APE和△BQF中，

，

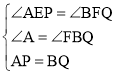∴△APE≌△BQF（AAS），

∴AE＝BF，PE＝QF且PE∥QF，

∴四邊形PEQF是平行四邊形，

∴DE＝EF，

∵EB+AE＝BE+BF＝AB，

∴DE＝AB，

又∵等邊△ABC的邊長為6，

∴DE＝3，

∴當點P、Q運動時，線段DE的長度不會改變．