
【題目】解答題
(1)【問題提出】
如圖①,已知△ABC是等腰三角形,點E在線段AB上,點D在直線BC上,且ED=EC,將△BCE繞點C順時針旋轉60°至△ACF連接EF
試證明:AB=DB+AF
(2)【類比探究】
如圖②,如果點E在線段AB的延長線上,其他條件不變,線段AB,DB,AF之間又有怎樣的數量關系?請說明理由
(3)如果點E在線段BA的延長線上,其他條件不變,請在圖③的基礎上將圖形補充完整,并寫出AB,DB,AF之間的數量關系,不必說明理由.
【答案】
(1)
證明:ED=EC=CF,
∵△BCE繞點C順時針旋轉60°至△ACF,
∴∠ECF=60°,∠BCA=60°,BE=AF,EC=CF,
∴△CEF是等邊三角形,
∴EF=EC,∠CEF=60°,
又∵ED=EC,
∴ED=EF,
∵△ABC是等腰三角形,∠BCA=60°,
∴△ABC是等邊三角形,
∴∠CAF=∠CBA=60°,
∴∠EAF=∠BAC+∠CAF=120°,∠DBE=120°,∠EAF=∠DBE,
∵∠CAF=∠CEF=60°,
∴A、E、C、F四點共圓,
∴∠AEF=∠ACF,
又∵ED=EC,
∴∠D=∠BCE,∠BCE=∠ACF,
∴∠D=∠AEF,
在△EDB和△FEA中,
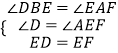 (AAS)
(AAS)
∴△EDB≌△FEA,
∴DB=AE,BE=AF,
∵AB=AE+BE,
∴AB=DB+AF
(2)
證明:AB=BD﹣AF;
延長EF、CA交于點G,
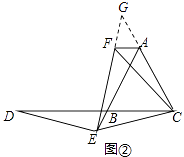
∵△BCE繞點C順時針旋轉60°至△ACF,
∴∠ECF=60°,BE=AF,EC=CF,
∴△CEF是等邊三角形,
∴EF=EC,
又∵ED=EC,
∴ED=EF,∠EFC=∠BAC=60°,
∵∠EFC=∠FGC+∠FCG,∠BAC=∠FGC+∠FEA,
∴∠FCG=∠FEA,
又∵∠FCG=∠ECD,∠D=∠ECD,
∴∠D=∠FEA,
由旋轉的性質,可得
∠CBE=∠CAF=120°,
∴∠DBE=∠FAE=60°,
在△EDB和△FEA中,
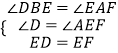 (AAS)
(AAS)
∴△EDB≌△FEA,
∴BD=AE,EB=AF,
∴BD=FA+AB,
即AB=BD﹣AF
(3)
證明:如圖③,
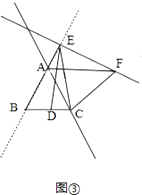 ,
,
ED=EC=CF,
∵△BCE繞點C順時針旋轉60°至△ACF,
∴∠ECF=60°,BE=AF,EC=CF,BC=AC,
∴△CEF是等邊三角形,
∴EF=EC,
又∵ED=EC,
∴ED=EF,
∵AB=AC,BC=AC,
∴△ABC是等邊三角形,
∴∠ABC=60°,
又∵∠CBE=∠CAF,
∴∠CAF=60°,
∴∠EAF=180°﹣∠CAF﹣∠BAC
=180°﹣60°﹣60°
=60°
∴∠DBE=∠EAF;
∵ED=EC,
∴∠ECD=∠EDC,
∴∠BDE=∠ECD+∠DEC=∠EDC+∠DEC,
又∵∠EDC=∠EBC+∠BED,
∴∠BDE=∠EBC+∠BED+∠DEC=60°+∠BEC,
∵∠AEF=∠CEF+∠BEC=60°+∠BEC,
∴∠BDE=∠AEF,
在△EDB和△FEA中,
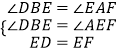 (AAS)
(AAS)
∴△EDB≌△FEA,
∴BD=AE,EB=AF,
∵BE=AB+AE,
∴AF=AB+BD,
即AB,DB,AF之間的數量關系是:
AF=AB+BD
【解析】(1)首先判斷出△CEF是等邊三角形,即可判斷出EF=EC,再根據ED=EC,可得ED=EF,∠CAF=∠BAC=60°,所以∠EAF=∠BAC+∠CAF=120°,∠DBE=120°,∠EAF=∠DBE;然后根據全等三角形判定的方法,判斷出△EDB≌△FEA,即可判斷出BD=AE,AB=AE+BF,所以AB=DB+AF.(2)首先判斷出△CEF是等邊三角形,即可判斷出EF=EC,再根據ED=EC,可得ED=EF,∠CAF=∠BAC=60°,所以∠EFC=∠FGC+∠FCG,∠BAC=∠FGC+∠FEA,∠FCG=∠FEA,再根據∠FCG=∠EAD,∠D=∠EAD,可得∠D=∠FEA;然后根據全等三角形判定的方法,判斷出△EDB≌△FEA,即可判斷出BD=AE,EB=AF,進而判斷出AB=BD﹣AF即可.(3)首先根據點E在線段BA的延長線上,在圖③的基礎上將圖形補充完整,然后判斷出△CEF是等邊三角形,即可判斷出EF=EC,再根據ED=EC,可得ED=EF,∠CAF=∠BAC=60°,再判斷出∠DBE=∠EAF,∠BDE=∠AEF;最后根據全等三角形判定的方法,判斷出△EDB≌△FEA,即可判斷出BD=AE,EB=AF,進而判斷出AF=AB+BD即可.
【考點精析】關于本題考查的等邊三角形的性質,需要了解等邊三角形的三個角都相等并且每個角都是60°才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】如圖所示,AB是⊙O的直徑,點C是 ![]() 的中點,∠COB=60°,過點C作CE⊥AD,交AD的延長線于點E
的中點,∠COB=60°,過點C作CE⊥AD,交AD的延長線于點E 
(1)求證:CE為⊙O的切線;
(2)判斷四邊形AOCD是否為菱形?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某養雞場有2500只雞準備對外出售.從中隨機抽取了一部分雞,根據它們的質量(單位:![]() ),繪制出如下的統計圖①和圖②.請根據相關信息,解答下列問題:
),繪制出如下的統計圖①和圖②.請根據相關信息,解答下列問題:

(Ⅰ)圖①中![]() 的值為 ;
的值為 ;
(Ⅱ)求統計的這組數據的平均數、眾數和中位數;
(Ⅲ) 根據樣本數據,估計這2500只雞中,質量為![]() 的約有多少只?
的約有多少只?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c圖象的一部分,其對稱軸是x=﹣1,且過點(﹣3,0),下列說法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ![]() ,y2)是拋物線上兩點,則y1<y2 , 其中說法正確的是( )
,y2)是拋物線上兩點,則y1<y2 , 其中說法正確的是( ) 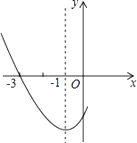
A.①②
B.②③
C.①②④
D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,△ABC的三個頂點坐標分別為A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)①畫出△ABC關于y軸對稱的△A1B1C1;
②畫出△ABC關于原點O成中心對稱的△A2B2C2;
(2)求△A2B2C2的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠BOC=9°,點A在OB上,且OA=1,按下列要求畫圖:
以A為圓心,1為半徑向右畫弧交OC于點A1,得第1條線段AA1;再以A1為圓心,1為半徑向右畫弧交OB于點A2,得第2條線段A1A2;再以A2為圓心,1為半徑向右畫弧交OC于點A3,得第3條線段A2A3;…這樣畫下去,直到得第n條線段,之后就不能再畫出符合要求的線段了,則n=______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 是等邊
是等邊![]() 內一點,
內一點, ![]() .將
.將![]() 繞點
繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 得
得![]() ,連接
,連接![]() .
.

(1)求證: ![]() 是等邊三角形;
是等邊三角形;
(2)當![]() 時,試判斷
時,試判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)探究:當![]() 為多少度時,
為多少度時, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠B=60°,對角線AC平分角∠BAD,點P是△ABC內一點,連接PA、PB、PC,若PA=6,PB=8,PC=10,則菱形ABCD的面積等于_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com