
 經過△ABC的三個頂點,點A坐標為(0,3),點B坐標為(2,3),點C在x軸的正半軸上.
經過△ABC的三個頂點,點A坐標為(0,3),點B坐標為(2,3),點C在x軸的正半軸上.
 。C(6,0)。
。C(6,0)。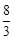 時,S取得最大值,最大值為1。
時,S取得最大值,最大值為1。 經過點A(0,3),B(2,3),
經過點A(0,3),B(2,3), ,解得:
,解得: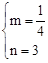 。
。 。
。 ,解得x=6或x=﹣4。
,解得x=6或x=﹣4。
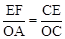 ,即
,即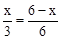 。
。
 ,即
,即 ,得
,得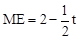 。
。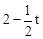 ,MH=DE=2。
,MH=DE=2。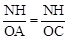 ,即
,即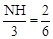 ,得NH=1。
,得NH=1。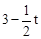 。
。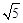 。
。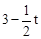 =
=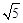 ,解得t=
,解得t=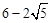 。
。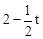 )2=(
)2=(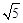 )2,解得t=2或t=6(不合題意,舍去)。
)2,解得t=2或t=6(不合題意,舍去)。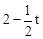 )2=(
)2=(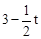 )2,解得t=1。
)2,解得t=1。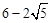 時,△DMN是等腰三角形。
時,△DMN是等腰三角形。
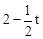 ,DN=
,DN=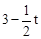 .
. ,解得
,解得 。
。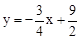 。
。 。
。 。
。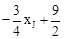 ,得
,得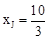 。
。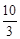 =t﹣
=t﹣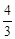 。
。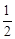 (ME+DN)•DE﹣
(ME+DN)•DE﹣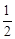 FK•FJ
FK•FJ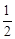 [(2﹣
[(2﹣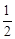 t)+(3﹣
t)+(3﹣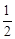 t)]×2﹣
t)]×2﹣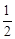 (
(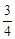 t﹣1)(t﹣
t﹣1)(t﹣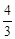 )
) .
.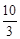 ,
,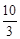 。
。 (2<t<
(2<t<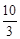 )。
)。 ,
,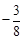 <0,且2<
<0,且2<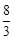 <
<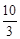 ,∴當t=
,∴當t=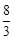 時,S取得最大值,最大值為1。
時,S取得最大值,最大值為1。

科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
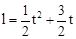 (t≥0),乙以4cm/s的速度勻速運動,半圓的長度為21cm.
(t≥0),乙以4cm/s的速度勻速運動,半圓的長度為21cm.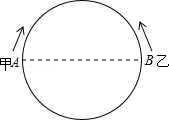
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
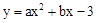 (a,b是常數)的圖象與x軸交于點A(﹣3,0)和點B(1,0),與y軸交于點C.動直線y=t(t為常數)與拋物線交于不同的兩點P、Q.
(a,b是常數)的圖象與x軸交于點A(﹣3,0)和點B(1,0),與y軸交于點C.動直線y=t(t為常數)與拋物線交于不同的兩點P、Q.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 的圖象與二次函數y=ax2+x-1的圖象相交于點(2,2)
的圖象與二次函數y=ax2+x-1的圖象相交于點(2,2)查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 (
( 是常數)
是常數) 軸只有一個交點,求
軸只有一個交點,求 的值;
的值; 在某反比例函數的圖像上,要使該反比例函數和二次函數
在某反比例函數的圖像上,要使該反比例函數和二次函數 都是
都是 隨
隨 的增大而增大,求
的增大而增大,求 應滿足的條件以及
應滿足的條件以及 的取值范圍;
的取值范圍; 與
與 軸交于
軸交于 兩點,且
兩點,且 ,
, ,在
,在 軸上,是否存在點P,使△ABP是直角三角形?若存在,求出點P及△ABP的面積;若不存在,請說明理由。
軸上,是否存在點P,使△ABP是直角三角形?若存在,求出點P及△ABP的面積;若不存在,請說明理由。查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
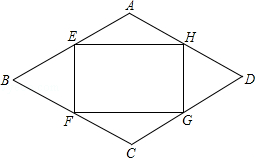
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com