
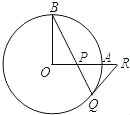
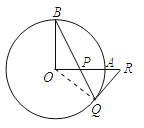
【題目】如圖,OA和OB是⊙O的半徑,OB=2,OA⊥OB,P是OA上任一點,BP的延長線交⊙O于點Q,過點Q的⊙O的切線交OA延長線于點R.
(1)求證:RP=RQ;
(2)若OP=PQ,求PQ的長.
【答案】(1)證明見解析(2)![]()
【解析】
(1)連接OQ,由QR為圓O的切線,得到∠OQR為90°,即∠OQB+∠PQR=90°,由OA與OB垂直,根據垂直的定義得到∠BOA=90°,所以∠B+∠BPO=90°,再根據對頂角相等及等角的余角相等,得到∠RPQ=∠RQP,根據“等角對等邊”得證;
(2)根據OP=PQ,由“等邊對等角”得到∠POQ=∠PQO,又根據半徑OB=OQ,再根據“等邊對等角”得到∠B=∠BQO,在三角形OBQ中,由∠BOA為直角,設出∠B=∠PQO=∠POQ=x,根據三角形的內角和定理列出關于x的方程,求出方程的解得到x的值,即為∠B的度數,又∠RPQ=∠BPO=60°,PR=QR,所以三角形PRQ為等邊三角形,所以PQ=QR,在直角三角形OQR中,根據30°的正切函數定義,由OQ=OB=2,即可求出QR的值,從而得到PQ的長.
(1)連接OQ.∵QR是切線,∴∠OQR=90°,∴∠BQO+∠PQR=90°.
∵OA⊥OB,∴∠BOA=90°,∴∠B+∠BPO=90°,又∠BPO=∠RPQ,∴∠B+∠RPQ=90°.
由OB=OQ得:∠B=∠BQO,∴∠RPQ=∠RQP,∴PR=QR;
(2)∵OP=PQ,∴∠POQ=∠PQO,
又OB=OQ,∴∠B=∠PQO,
設∠B=∠PQO=∠POQ=x,又∠BOP=90°,
根據三角形內角和定理得:
∠B+∠BOP+∠POQ+∠PQO=180°,即x+90°+x+x=180°,
解得:x=30°,即∠B=30°,∴∠RPQ=∠BPO=60°,又PR=QR,∴△PQR為等邊三角形,即PQ=QR=PR,
在直角三角形OQR中,OQ=OB=2,
根據銳角三角函數定義得:
![]() .
.


科目:初中數學 來源: 題型:
【題目】(2016湖南省株洲市)某市對初二綜合素質測評中的審美與藝術進行考核,規定如下:考核綜合評價得分由測試成績(滿分100分)和平時成績(滿分100分)兩部分組成,其中測試成績占80%,平時成績占20%,并且當綜合評價得分大于或等于80分時,該生綜合評價為A等.
(1)孔明同學的測試成績和平時成績兩項得分之和為185分,而綜合評價得分為91分,則孔明同學測試成績和平時成績各得多少分?
(2)某同學測試成績為70分,他的綜合評價得分有可能達到A等嗎?為什么?
(3)如果一個同學綜合評價要達到A等,他的測試成績至少要多少分?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中點,E是AD的中點.過點A作AF∥BC交BE的延長線于點F.
,D是BC的中點,E是AD的中點.過點A作AF∥BC交BE的延長線于點F.

(1)求證:△AEF≌△DEB;
(2)證明四邊形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,反比例函數y=![]() (x<0)的圖象經過矩形OABC的對角線AC的中點M,分別與AB,BC交于點D、E,若BD=3,OA=4,則k的值為_____.
(x<0)的圖象經過矩形OABC的對角線AC的中點M,分別與AB,BC交于點D、E,若BD=3,OA=4,則k的值為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
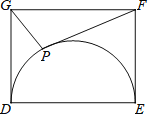
【題目】在△ABC中,若O為BC邊的中點,則必有:AB2+AC2=2AO2+2BO2成立.依據以上結論,解決如下問題:如圖,在矩形DEFG中,已知DE=4,EF=3,點P在以DE為直徑的半圓上運動,則PF2+PG2的最小值為( )
A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題提出
(1)如圖①,在△ABC中,∠A=120°,AB=AC=5,則△ABC的外接圓半徑R的值為 .
問題探究
(2)如圖②,⊙O的半徑為13,弦AB=24,M是AB的中點,P是⊙O上一動點,求PM的最大值.
問題解決
(3)如圖③所示,AB、AC、BC是某新區的三條規劃路其中,AB=6km,AC=3km,∠BAC=60°,BC所對的圓心角為60°.新區管委會想在BC路邊建物資總站點P,在AB、AC路邊分別建物資分站點E、F.也就是,分別在![]() 、線段AB和AC上選取點P、E、F.由于總站工作人員每天要將物資在各物資站點間按P→E→F→P的路徑進行運輸,因此,要在各物資站點之間規劃道路PE、EF和FP.為了快捷環保和節約成本要使得線段PE、EF、FP之和最短,試求PE+EF+FP的最小值(各物資站點與所在道路之間的距離、路寬均忽略不計).
、線段AB和AC上選取點P、E、F.由于總站工作人員每天要將物資在各物資站點間按P→E→F→P的路徑進行運輸,因此,要在各物資站點之間規劃道路PE、EF和FP.為了快捷環保和節約成本要使得線段PE、EF、FP之和最短,試求PE+EF+FP的最小值(各物資站點與所在道路之間的距離、路寬均忽略不計).



圖① 圖② 圖③
查看答案和解析>>
科目:初中數學 來源: 題型:
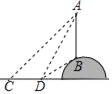
【題目】如圖,為了測量小山頂的鐵塔AB高度,王華和楊麗在平地上的C點處測得A點的仰角為45°,向前走了18m后到達D點,測得A點的仰角為60°,B點的仰角為30°
(1)求證:AB=BD;
(2)求證鐵塔AB的高度.(結果精確到0.1米,其中![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC中,BO、CO是角平分線.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度數,并說明理由.
(2)題(1)中,如將“∠ABC=50°,∠ACB=60°”改為“∠A=70°”,求∠BOC的度數.
(3)若∠A=n°,求∠BOC的度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com