
【題目】數軸上有![]() ,
,![]() ,
,![]() 三點,給出如下定義:若其中一個點與其它兩個點的距離恰好滿足2倍的數量關系,則稱該點是其它兩個點的“關聯點”.例如數軸上點
三點,給出如下定義:若其中一個點與其它兩個點的距離恰好滿足2倍的數量關系,則稱該點是其它兩個點的“關聯點”.例如數軸上點![]() ,
,![]() ,
,![]() 所表示的數分別為1, 3,4,此時點
所表示的數分別為1, 3,4,此時點![]() 是點
是點![]() ,
,![]() 的“關聯點”.
的“關聯點”.
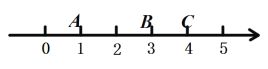
(1)若點![]() 表示數-2,點
表示數-2,點![]() 表示數1,下列各數-1, 2, 4, 6所對應的點分別是
表示數1,下列各數-1, 2, 4, 6所對應的點分別是![]() ,
,![]() ,
,![]() ,
,![]() ,其中是點
,其中是點![]() ,
,![]() 的“關聯點”的是
的“關聯點”的是
(2)點![]() 表示數-10,點
表示數-10,點![]() 表示數15,
表示數15,![]() 為數軸上一個動點:
為數軸上一個動點:
①若點![]() 在點
在點![]() 的左側,且點
的左側,且點![]() 是點
是點![]() ,
,![]() 的“關聯點”,求此時點
的“關聯點”,求此時點![]() 表示的數;
表示的數;
②若點![]() 在點
在點![]() 的右側,點
的右側,點![]() ,
,![]() ,
,![]() 中,有一個點恰好是其它兩個點的“關聯點”,請直接寫出此時點
中,有一個點恰好是其它兩個點的“關聯點”,請直接寫出此時點![]() 表示的數.
表示的數.
【答案】(1)C1或![]() ;(2)①-35或
;(2)①-35或![]() 或
或![]() ;②40、
;②40、![]() 、65.
、65.
【解析】
(1)根據題意由兩個點的“關聯點”的定義,求得CA與BC的關系,得到答案;
(2)①由題意設點P表示的數為x,根據PA,PB成2倍關系列方程求解;
②分當P為A、B關聯點、A為P、B關聯點、B為A、P關聯點、B為P、A關聯點四種可能列方程解答.
解:(1)C1A=1,C1B=2,C1B=2C1A,故C1符合題意;
C2A=4,C2B=1,故C2不符合題意;
C3A=6,C3B=3,C3A=2C3B,故C3符合題意;
C4A=8,C4B=5,故C4不符合題意.
故答案為:C1或![]() .
.
(2)①設點P表示的數為x,
當P點在點A左側時,有PB=2PA,則 15-x=2(-10-x),解得 x=-35.所以點P表示的數為-35;
當P點在AB之間時,分別有PB=2PA和PA=2PB,列方程分別解得P點表示的數為![]() 和
和![]() ;
;
綜上所述,當點P在點B的左側時,點P表示的數為-35或![]() 或
或![]() .
.
②點![]() 在點
在點![]() 的右側時,分三種情況:
的右側時,分三種情況:
當P為A、B關聯點時,設點P表示的數為x,
∵PA=2PB,
∴x+10=2(x-15),
解得x=40,
即此時點P表示的數40;
當B為A、P關聯點時:設點P表示的數為x,
∵AB=2PB,
∴25=2(x-15),
解得x=![]() ,
,
即此時點P表示的數![]() ;
;
當B為P、A關聯點時:設點P表示的數為x,
∵PB=2AB,
∴x-15=50,
解得x=65,
即此時點P表示的數65,
故答案為:40、![]() 、65.
、65.


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】定義:只有一組對角是直角的四邊形叫做損矩形,連結它的兩個非直角頂點的線段叫做這個損矩形的直徑.
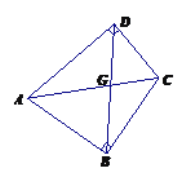
(1)如圖,損矩形![]() 中,
中,![]() ,則該損矩形的直徑是線段______.
,則該損矩形的直徑是線段______.
(2)探究:在上述損矩形![]() 內,是否存在點
內,是否存在點![]() ,使
,使![]() 四個點都在以
四個點都在以![]() 為圓心的同一圓上,若存在,請指出點
為圓心的同一圓上,若存在,請指出點![]() 的具體位置___________________________;若不存在,請說明理由.
的具體位置___________________________;若不存在,請說明理由.
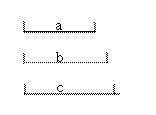
(3)實踐:已知如圖三條線段![]() ,求作相鄰三邊長順次為
,求作相鄰三邊長順次為![]() 的損矩形
的損矩形![]() (尺規作圖,保留作圖痕跡).
(尺規作圖,保留作圖痕跡).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如下圖中的小正方形的大小相等,圖1只有一個小正方形;圖2是由4個小正方形構成的一個正方形;圖3是由9個小正方形構成的一個正方形,…以此類推,每一個圖形都是由小正方形構成的大正方形. 回答下列問題:
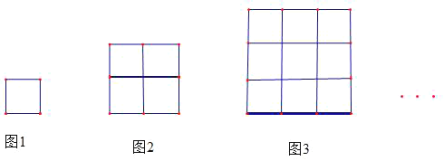
(1)圖2比圖1多________個小正方形,圖3比圖2多________個小正方形.
(2)圖![]() 比圖
比圖![]() 多________個小正方形(用含
多________個小正方形(用含![]() 的式子表示)
的式子表示)
(3)猜想![]() ________.
________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知兩直線![]() 與
與![]()
(1)在同一平面直角坐標系中作出兩直線的圖象;
(2)求出兩直線的交點;
(3)根據圖象指出x為何值時,![]() ;
;
(4)求這兩條直線與x軸圍成的三角形面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
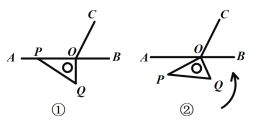
【題目】如圖①,![]() 為直線
為直線![]() 上一點,作射線
上一點,作射線![]() ,使
,使![]() ,將一個直角三角尺如圖擺放,直角頂點在點
,將一個直角三角尺如圖擺放,直角頂點在點![]() 處,一條直角邊
處,一條直角邊![]() 在射線
在射線![]() 上. 將圖
上. 將圖![]() 中的三角尺繞點
中的三角尺繞點![]() 以每秒10°的速度按逆時針方向旋轉(如圖②所示),在旋轉一周的過程中,第
以每秒10°的速度按逆時針方向旋轉(如圖②所示),在旋轉一周的過程中,第![]() 秒時,
秒時,![]() 所在直線恰好平分
所在直線恰好平分![]() ,則
,則![]() 的值為_________.
的值為_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)點P從點A開始沿AB邊向B以1cm/s的速度移動,點Q從B點開始沿BC邊向點C以2cm/s的速度移動.如果P,Q分別從A,B同時出發,經過幾秒,使△PBQ的面積等于8cm2?
(2)點P從點A開始沿AB邊向B以1cm/s的速度移動,點Q從B點開始沿BC邊向點C以2cm/s的速度移動.如果P,Q分別從A,B同時出發,線段PQ能否將△ABC分成面積相等的兩部分?若能,求出運動時間;若不能說明理由.
(3)若P點沿射線AB方向從A點出發以1cm/s的速度移動,點Q沿射線CB方向從C點出發以2cm/s的速度移動,P,Q同時出發,問幾秒后,△PBQ的面積為1?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校初三(1)班50名學生需要參加體育“五選一”自選項目測試,班上學生所報自選項目的情況統計表如下:
自選項目 | 人數 | 頻率 |
立定跳遠 | 9 | 0.18 |
三級蛙跳 | 12 | a |
一分鐘跳繩 | 8 | 0.16 |
投擲實心球 | b | 0.32 |
推鉛球 | 5 | 0.10 |
合計 | 50 | 1 |
(1)求a,b的值;
(2)若將各自選項目的人數所占比例繪制成扇形統計圖,求“一分鐘跳繩”對應扇形的圓心角的度數;
(3)在選報“推鉛球”的學生中,有3名男生,2名女生,為了了解學生的訓練效果,從這5名學生中隨機抽取兩名學生進行推鉛球測試,求所抽取的兩名學生中至多有一名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
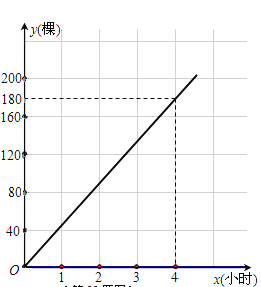
【題目】為了“綠化環境,美化家園”,3月12日(植樹節)上午8點,某校901、902班同學同時參加義務植樹.901班同學始終以同一速度種植樹苗,種植樹苗的棵數y1與種植時間x(小時)的函數圖象如圖所示;902班同學開始以1小時種植40棵的速度工作了1.5小時后,因需更換工具而停下休息半小時,更換工具后種植速度提高至原來的1.5倍.
(1)求902班同學上午11點時種植的樹苗棵數;
(2)分別求出901班種植數量y1、902班種植數量y2與種植時間x(小時)之間的函數關系式,并在所給坐標系上畫出y2關于x的函數圖象;
(3)已知購買樹苗不多于120棵時,每棵樹苗的價格是20元;購買樹苗超過120棵時,超過的部分每棵價格17元.若本次植樹所購樹苗的平均成本是18元,則兩班同學上午幾點可以共同完成本次植樹任務?
【答案】(1)120棵;(2)見解析;(3)兩班同學上午12點可以共同完成本次植樹任務.
【解析】分析:![]() 直接進行計算即可.
直接進行計算即可.
![]() 用待定系數法求一次函數解析式即可, 902班的要分成3段.
用待定系數法求一次函數解析式即可, 902班的要分成3段.
![]() 當x=2時,兩班同學共植樹150棵,
當x=2時,兩班同學共植樹150棵,![]() 平均成本:不符合題意;,x>2,兩班共植樹(105x-60)棵.列出方程
平均成本:不符合題意;,x>2,兩班共植樹(105x-60)棵.列出方程![]() 求解即可.
求解即可.
詳解:(1)902班同學上午11點時種植的樹苗棵數為:
![]() (棵)
(棵)
(2)由圖可知,y1是關于x的正比例函數,可設y1=k1x,經過(4,180),
代入可得![]()
∴![]() (x≥0),
(x≥0),
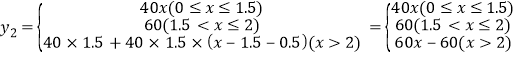 ,
,
y2關于x的函數圖象如圖所示.
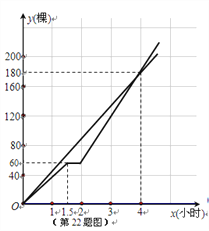
(3)當x=2時,兩班同學共植樹150棵,
![]() 平均成本:
平均成本:
所以,x>2,兩班共植樹(105x-60)棵.
![]() 由題意可得:
由題意可得:
解得:x=4.
![]() ,
,
所以,兩班同學上午12點可以共同完成本次植樹任務.
點睛:考查了待定系數法求一次函數解析式,一元一次方程的應用,注意分類討論
的數學思想方法.
【題型】解答題
【結束】
23
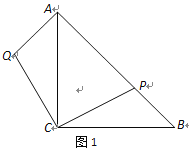
【題目】在等腰直角△ABC中,,AC=BC,點P在斜邊AB上(AP>BP).作AQ⊥AB,且AQ=BP,連結CQ(如圖1).
(1)求證:△ACQ≌△BCP;
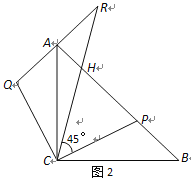
(2)延長QA至點R,使得∠RCP=45°,RC與AB交于點H,如圖2.
①求證:CQ2=QA·QR ;
②判斷三條線段AH、HP、PB的長度滿足的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點D是BC邊的中點,
,點D是BC邊的中點,![]() 于點E,
于點E,![]() 于點F.
于點F.

(1)![]() ________(用含α的式子表示)
________(用含α的式子表示)
(2)作射線DM與邊AB交于點M,射線DM繞點D順時針旋轉![]() ,與AC邊交于點N.根據條件補全圖形,并寫出DM與DN的數量關系,請說明理由.
,與AC邊交于點N.根據條件補全圖形,并寫出DM與DN的數量關系,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com